
【题目】如图,矩形ABCD中,对角线AC、BD相交于点O,点P是线段AD上一动点(不与与点D重合),PO的延长线交BC于Q点.
(1)求证:四边形PBQD为平行四边形.
(2)若AB=6cm,AD=8cm,P从点A出发.以1cm/秒的速度向点D匀速运动.设点P运动时间为t秒,问四边形PBQD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.

【答案】(1)详见解析;(2)点P运动时间为![]() 秒时,四边形PBQD是菱形.
秒时,四边形PBQD是菱形.
【解析】
(1)依据矩形的性质和平行线的性质,通过全等三角形的判定定理判定△POD≌△QOB,所以OP=OQ,则四边形PBQD的对角线互相平分,故四边形PBQD为平行四边形.
(2)点P从点A出发运动t秒时,AP=tcm,PD=(4-t)cm.当四边形PBQD是菱形时,PB=PD=(4-t)cm.在直角△ABP中,根据勾股定理得AP2+AB2=PB2,即t2+32=(4-t)2,由此可以求得t的值.
(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠PDO=∠QBO,
在△POD和△QOB中,
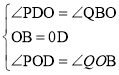
∴△POD≌△QOB(ASA),
∴OP=OQ;
又∵OB=OD
∴四边形PBQD为平行四边形;
(2)答:能成为菱形;
证明:t秒后AP=t,PD=8﹣t,
若四边形PBQD是菱形,
∴PD=BP=8﹣t,
∵四边形ABCD是矩形,
∴∠A=90°,
在Rt△ABP中,由勾股定理得:AB2+AP2=BP2,
即62+t2=(8﹣t)2,
解得:t=![]() .
.
即点P运动时间为![]() 秒时,四边形PBQD是菱形.
秒时,四边形PBQD是菱形.


科目:初中数学 来源: 题型:
【题目】 在平面直角坐标系xOy中,O为坐标原点,四边形OABC的顶点A在x轴的正半轴上,OA=4,OC=2,点P,点Q分别是边BC,边AB上的点,连结AC,PQ,点B1是点B关于PQ的对称点.
(1)若四边形OABC为长方形,如图1,
①求点B的坐标;
②若BQ=BP,且点B1落在AC上,求点B1的坐标;
(2)若四边形OABC为平行四边形,如图2,且OC⊥AC,过点B1作B1F∥x轴,与对角线AC,边OC分别交于点E,点F.若B1E:B1F=1:3,点B1的横坐标为m,求点B1的纵坐标(用含m的代数式表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了鼓励居民节约用水,决定实行两级收费制度.若每月用水量不超过14吨,则每吨按政府补贴优惠价a元收费;若每月用水量超过14吨,则超过部分每吨按市场调节价b元收费.小刘家3月份用水10吨,交水费20元;4月份用水16吨,交水费35元.
(1)求每吨水的政府补贴优惠价和市场调节价分别是多少?
(2)设每月用水量为x吨,应交水费为y元,请写出y与x之间的函数关系式;
(3)小刘预计他家5月份用水不会超过22吨,那么小刘家5月份最多交多少元水费?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“绿满鄂南”行动中,某社区计划对面积为1800m2的区域进行绿化.经投标,由甲、乙两个工程队来完成,已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为400m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积.
(2)设甲工程队施工x天,乙工程队施工y天,刚好完成绿化任务,求y与x的函数解析式.
(3)若甲队每天绿化费用是0.6万元,乙队每天绿化费用为0.25万元,且甲乙两队施工的总天数不超过26天,则如何安排甲乙两队施工的天数,使施工总费用最低?并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.

(1)求证:△BDF是等腰三角形;
(2)如图2,过点D作DG∥BE,交BC于点G,连接FG交BD于点O.
①判断四边形BFDG的形状,并说明理由;
②若AB=6,AD=8,求FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果把一个自然数各数位上的数字从最高位到个位依次排出的一个数,与从个位到最高位依次排出的一个数完全相同,那么我们把这样的自然数称为“和谐数”,例如![]() ,
,![]() ,
,![]() ,
,![]() 都是“和谐数”.请你解答以下问题:
都是“和谐数”.请你解答以下问题:
(![]() )设一个四位“和谐数”个位上的数字
)设一个四位“和谐数”个位上的数字![]() ,十位上的数字为
,十位上的数字为![]() ,请你用含有
,请你用含有![]() 、
、![]() 的代数式表示出这个四位数.
的代数式表示出这个四位数.
(![]() )请说明任意一个四位“和谐数”都能被
)请说明任意一个四位“和谐数”都能被![]() 整除.
整除.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上.
(1)求证:△ABF∽△DFE;
(2)如果AB=12,BC=15,求tan∠FBE的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A5B5A6的边长为( )

A.6B.16C.32D.64
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC、BD相交于点O,E是OB的中点,过点B作BF∥AC交AE的延长线于点F,连接CF.

(1)求证:△AOE≌△FBE;
(2)求证:四边形BOCF是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com