
【题目】如图,将ABCD沿过点A的直线l折叠,使点D落到AB边上的点D'处,直线l交CD边于点E,连接BE.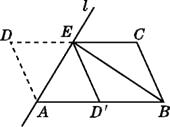
(1)求证:四边形BCED'是平行四边形;
(2)若BE平分∠ABC,求证:AB2=AE2+BE2.
【答案】
(1)证明:由折叠的性质可得∠DAE=∠D'AE,∠DEA=∠D'EA,DA=D'A.
∵DE∥AD',∴∠DEA=∠EAD',
∴∠DAE=∠EAD'=∠DEA.
∴DE=DA=AD'.
∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC
∴CE∥D'B,CE=D'B,
∴四边形BCED'是平行四边形
(2)证明:∵BE平分∠ABC,∴∠CBE=∠EBA.
∵AD∥BC,∴∠DAB+∠CBA=180°.
∵∠DAE=∠BAE,∴∠EAB+∠EBA=90°.
∴∠AEB=90°.∴AB2=AE2+BE2
【解析】(1)根据折叠的性质得出∠DAE=∠D'AE,∠DEA=∠D'EA,DA=D'A.,再根据平行四边形的性质及平行线的性质证明DE=AD',就可证明四边形ABCD是平行四边形,再证明CE∥D'B,CE=D'B,,就可证明四边形BCED'是平行四边形。
(2)根据角平分线的定义及平行线的性质证明△ABE是直角三角形,再利用勾股定理即可证得结论。


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案科目:初中数学 来源: 题型:
【题目】下列计算正确的是( )
A.6a23ab=9a3b
B.(2ab2)(﹣2ab)=﹣4a2b3
C.(ab)2(﹣a2b)=﹣a3b3
D.(﹣3a2b)(﹣3ab)=﹣6a3b2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC,BD相交于点O,E,F是对角线AC上的两点,当点E,F满足下列哪个条件时,四边形DEBF不一定是平行四边形( )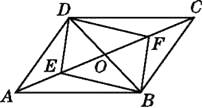
A.OE=OF
B.DF=BE
C.AE=CF
D.∠AEB=∠CFD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知:矩形ABCD中,AC、BD是对角线,分别延长AD至E,延长CD至F,使得DE=AD,DF=CD.
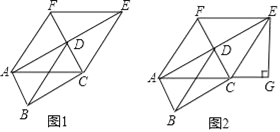
(1)求证:四边形ACEF为菱形.
(2)如图2,过E作EG⊥AC的延长线于G,若AG=8,cos∠ECG=![]() ,则AD= (直接填空)
,则AD= (直接填空)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=5cm,∠BAC=60°,动点M从点B出发,在BA边上以每秒2cm的速度向点A匀速运动,同时动点N从点C出发,在CB边上以每秒![]() cm的速度向点B匀速运动,设运动时间为t秒(0≤t≤5),连接MN.
cm的速度向点B匀速运动,设运动时间为t秒(0≤t≤5),连接MN.
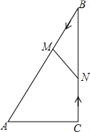
(1)若BM=BN,求t的值;
(2)若△MBN与△ABC相似,求t的值;
(3)当t为何值时,四边形ACNM的面积最小?并求出最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com