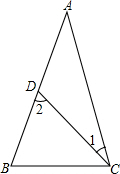
如图.在△ABC中.已知∠A=∠1.∠2=∠B.∠ABC=∠ACB.求∠ACB的度数．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

18．

如图，在△ABC中，已知∠A=∠1，∠2=∠B，∠ABC=∠ACB，求∠ACB的度数．

分析设∠A=∠1=x，则∠2=2x，再由∠2=∠B，∠ABC=∠ACB可知∠B=∠ACB=2x，根据三角形内角和定理求出x的值即可得出结论．

解答解：设∠A=∠1=x，
∵∠2是△ACD的外角，
∴∠2=2x．
∵∠2=∠B，∠ABC=∠ACB，
∴∠B=∠ACB=2x．
∵∠A+∠B+∠ACB=180°，即x+2x+2x=180°，解得x=36°，
∴∠ACB=2x=72°．

点评本题考查的是三角形内角和定理，熟知三角形内角和是180°是解答此题的关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：选择题

8．据统计，2014年杭州市全社会用于基础建设的资金约为100553000000元，这个数用科学记数法表示为（　　）元．

A．

1.00553×10⁹

B．

1.00553×10¹⁰

C．

1.00553×10¹¹

D．

1.00553×10¹²

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

9．下列命题中是假命题的是（　　）

	A．	垂直于弦的直径平分弦
	B．	若a＞b，c＞0，则ac＞bc
	C．	反比例函数y=$\frac{k}{x}$，当k＞0时，y随x的增大而减少
	D．	对角线互相平分且垂直的四边形是菱形

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

6．

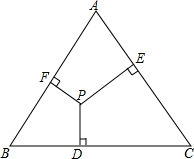有一块等边三角形的空地，小明和小亮想在这块空地上找到一点，使得这一点到三边的距离之和最短，他们做了几次实验，发现无论三角形内的哪一点到三边的距离之和都是相等的．于是他们编了一道几何题：如图，已知点P为正△ABC内一点，点P到BC，CA，AB的距离分别为PD，PE，PF，试说明PD+PE+PF总是一个定值．这个定值与什么有关？你发现这个事实了吗？你能解出他们编的数学问题吗？

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

13．如图1，△ACB的顶点C在等腰直角△ADE的边DE上，∠EAD=90°，∠CAE=∠DCB=∠BAD
（1）求证：AC=AB；
（2）求证：CE²+CD²=2AC²；
（3）如图2，过点C作CF⊥AE于点F，点G为BC中点，若CE=$\sqrt{2}$，∠BAD=30°，请直接写出线段FG的长．