
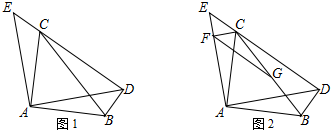
分析 (1)根据∠CAE=∠DCB,得出∠EAD=∠CAB=90°,利用三角形的外角性质得出∠ACB=∠E=45°解答即可;(2)根据等边三角形的性质就可以得出△AEC≌△ABD,就可以得出CE=BD,∠E=∠BDA,由等腰直角三角形的性质就可以得出∠CDB=90°,由勾股定理就可以得出结论;
(3)根据30°的直角三角形性质和等腰直角三角形的性质解答即可.
解答 证明:(1)∵∠CAE=∠DCB,
∴∠EAD=∠CAB=90°,
∵∠CAE=∠DCB,
∵∠ACD=∠E+∠CAE=∠DCB+∠ACB,
∴∠ACB=∠E=45°,
∴△CAB是等腰直角三角形,
∴AC=AB;
(2)∵△CAB与△EAD都是等腰直角三角形,
∴∠EAD=∠CAB=90°,∠E=∠CDA=∠ACB=45°,
EA=DA,CA=BA,CA2+BA2=CB2,
∴2AC2=CB2.∠EAD-CAD=∠CAB-∠CAD,
∴∠CAE=∠BAD
在△CEA和△BDA中,
$\left\{\begin{array}{l}{AC=BA}\\{∠CAE=∠BAD}\\{EA=DA}\end{array}\right.$,
∴△CEA≌△BDA(SAS).
∴CE=BD,∠E=∠BDA.
∴∠BDA=45°,
∴∠BDA+∠CDA=90°,
即∠CDB=90°.
∴CD2+BD2=CB2,
∴CD2+CE2=2AC2;
(3)∵CE=BD=$\sqrt{2}$,∠BAD=30°,∠CDB=90°,
∴BC=2$\sqrt{2}$,
∵CF⊥AE于点F,CE=$\sqrt{2}$,∠E=45°,
∴CF=1,CG=$\sqrt{2}$,
∴FG=2.
点评 本题考查了等腰直角三角形的性质的运用,直角三角形的判定及性质的运用,勾股定理的运用,全等三角形的判定及性质的运用,解答时证明三角形全等是关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
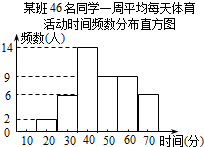 某班体育委员调查了本班46名同学一周的平均每天体育活动时间,并制作了如图所示的频数分布直方图,从直方图中可以看出,该班同学这一周平均每天体育活动时间的中位数在第4组,众数依次是在第3组.(从左至右数)
某班体育委员调查了本班46名同学一周的平均每天体育活动时间,并制作了如图所示的频数分布直方图,从直方图中可以看出,该班同学这一周平均每天体育活动时间的中位数在第4组,众数依次是在第3组.(从左至右数)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 正数 | B. | 负数 | C. | 非正数 | D. | 非负数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
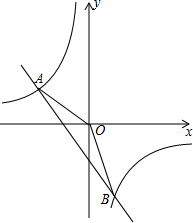 如图,已知反比例函数y1=$\frac{m}{x}$的图象与一次函数y2=kx+b的图象交于两点A(-2,1),B(a,-2).
如图,已知反比例函数y1=$\frac{m}{x}$的图象与一次函数y2=kx+b的图象交于两点A(-2,1),B(a,-2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
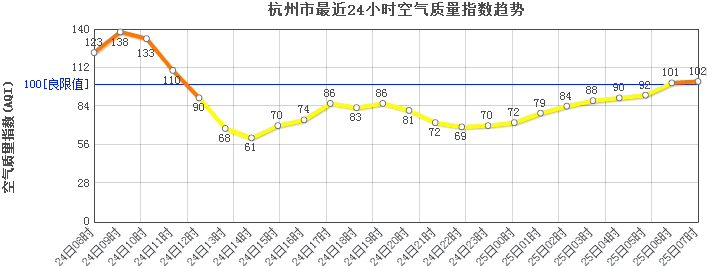
| A. | 在这个24小时中,AQI的值超过良限值时段是24日08时至24日12时 | |
| B. | 在这个24小时中,AQI对应的颜色为黄色的时段持续了20小时以上 | |
| C. | 在这个24小时中,AQI的最大值和最小值的差为77 | |
| D. | 建议中老年朋友在25日06时至07时进行晨练 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 购买香蕉数 | 不超过20千克 | 20千克以上 |
| 每千克价格 | 6元 | 5元 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com