
 已知点A、B分别在反比例函数y=$\frac{2}{x}$(x>0),y=$\frac{k}{x}$(x>0)的图象上,且OA⊥OB,tanB=$\frac{1}{2}$,则k=-8.
已知点A、B分别在反比例函数y=$\frac{2}{x}$(x>0),y=$\frac{k}{x}$(x>0)的图象上,且OA⊥OB,tanB=$\frac{1}{2}$,则k=-8. 分析 过点A作AC⊥y轴于点C,过点B作BD⊥y轴于点D,根据角与角之间的关系即可得出△AOC∽△OBD,由此即可得出$\frac{{S}_{△AOC}}{{S}_{△OBD}}$=$(\frac{AO}{OB})^{2}$,再根据反比例函数系数k的几何意义以及tanB=$\frac{1}{2}$即可得出关于k的分式方程,解之即可得出结论.
解答 解:过点A作AC⊥y轴于点C,过点B作BD⊥y轴于点D,如图所示.
∵AC⊥y轴,BD⊥y轴,OA⊥OB,
∴∠ACD=∠ODB=90°,∠AOB=90°.
∵∠OAC+∠AOC=90°,∠BOD+∠OBD=90°,∠AOC+∠BOD=180°-90°=90°,
∴∠AOC=∠OBD,
∴△AOC∽△OBD,
∴$\frac{{S}_{△AOC}}{{S}_{△OBD}}$=$(\frac{AO}{OB})^{2}$.
∵反比例函数y=$\frac{k}{x}$在第二象限有图象,
∴k<0.
∵tanB=$\frac{1}{2}$,S△AOC=$\frac{1}{2}$×2=1,S△OBD=$\frac{1}{2}$|k|=-$\frac{1}{2}$k,
∴$\frac{1}{-\frac{1}{2}k}$=$\frac{1}{4}$,解得:k=-8,
经检验:k=-8是方程$\frac{1}{-\frac{1}{2}k}$=$\frac{1}{4}$的解.
故答案为:-8.
点评 本题考查了反比例函数系数k的几何意义、相似三角形的判定与性质以及解直角三角形,根据反比例函数系数k的几何意义结合相似三角形的性质找出关于k的分式方程是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | x6÷x2=x3 | B. | 2x-1=$\frac{1}{2x}$ | C. | (-2x3)2=4x6 | D. | -2a2•a3=-2a6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
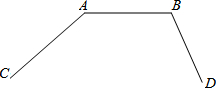 如图,已知三段公路(线段AB,以及射线AC、BD),请在AB的下方区域用尺规作一点P,使P点到三条公路的距离相等(保留作图痕迹,不写作法).
如图,已知三段公路(线段AB,以及射线AC、BD),请在AB的下方区域用尺规作一点P,使P点到三条公路的距离相等(保留作图痕迹,不写作法).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com