
【题目】如图,一次函数y=kx+b(k≠0)与反比例函数y= ![]() (m≠0)的图象有公共点A(1,a)、D(﹣2,﹣1).直线l与x轴垂直于点N(3,0),与一次函数和反比例函数的图象分别交于点B、C.
(m≠0)的图象有公共点A(1,a)、D(﹣2,﹣1).直线l与x轴垂直于点N(3,0),与一次函数和反比例函数的图象分别交于点B、C.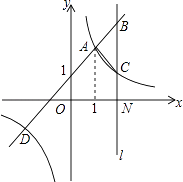
(1)求一次函数与反比例函数的解析式;
(2)根据图象回答,x在什么范围内,一次函数的值大于反比例函数的值;
(3)求△ABC的面积.
【答案】
(1)
解:∵反比例函数经过点D(﹣2,﹣1),
∴把点D代入y= ![]() (m≠0),
(m≠0),
∴﹣1= ![]() ,
,
∴m=2,
∴反比例函数的解析式为:y= ![]() ,
,
∵点A(1,a)在反比例函数上,
∴把A代入y= ![]() ,得到a=
,得到a= ![]() =2,
=2,
∴A(1,2),
∵一次函数经过A(1,2)、D(﹣2,﹣1),
∴把A、D代入y=kx+b (k≠0),得到: ![]() ,
,
解得: ![]() ,
,
∴一次函数的解析式为:y=x+1;
(2)
解:据图可知:当﹣2<x<0或x>1时,一次函数的值大于反比例函数的值;
(3)
解:过点A作AE⊥x轴交x轴于点E,
∵直线l⊥x轴,N(3,0),
∴设B(3,p),C(3,q),
∵点B在一次函数上,
∴p=3+1=4,
∵点C在反比例函数上,
∴q= ![]() ,
,
∴S△ABC= ![]() BCEN=
BCEN= ![]() ×(4﹣
×(4﹣ ![]() )×(3﹣1)=
)×(3﹣1)= ![]() .
.
【解析】(1)由反比例函数经过点D(﹣2,﹣1),即可求得反比例函数的解析式;然后求得点A的坐标,再利用待定系数法求得一次函数的解析式;(2)结合图象求解即可求得x在什么范围内,一次函数的值大于反比例函数的值;(3)首先过点A作AE⊥x轴交x轴于点E,由直线l与x轴垂直于点N(3,0),可求得点E,B,C的坐标,继而求得答案.


科目:初中数学 来源: 题型:
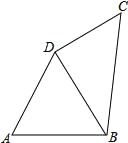
【题目】如图,在四边形ABCD中,AB=AD=8,∠A=60°,∠ADC=150°,四边形ABCD的周长为32.
(1)求∠BDC的度数;
(2)四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,现将一张矩形ABCD的纸片一角折叠,若能使点D落在AB边上F处,折痕为CE,恰好∠AEF=60°,延长EF交CB的延长线于点G. 
(1)求证:△CEG是等边三角形;
(2)若矩形的一边AD=3,求另一边AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC的平分线BF与△ABC的外角平分线CF相交于点F,过F作DF∥BC,交AB于D,交AC于E。

(1)写出图中所有的等腰三角形,并选择其中一个说明理由。
(2)直接写出BD,CE,DE之间的数量关系。
(3)若DE=5cm,CE=8cm,BF=24cm,求△BDF的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,E是AD上一点,AE=AB,过点E作直线EF,在EF上取一点G,使得∠EGB=∠EAB,连接AG.
(1)如图1,当EF与AB相交时,若∠EAB=60°,求证:EG=AG+BG;
(2)如图2,当EF与AB相交时,若∠EAB=α(0°<α<90°),请你直接写出线段EG、AG、BG之间的数量关系(用含α的式子表示);
(3)如图3,当EF与CD相交时,且∠EAB=90°,请你写出线段EG、AG、BG之间的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若四边形ABCD、四边形GFED都是正方形,AD=4, ![]() ,当正方形GFED绕D旋转到如图的位置,点F在边AD上,延长CE交AG于H,交AD于M.则CM的长为 .
,当正方形GFED绕D旋转到如图的位置,点F在边AD上,延长CE交AG于H,交AD于M.则CM的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(根据市教委提出的学生每天体育锻炼不少于1小时的要求,为确保阳光体育运动时间得到落实,某校对九年级学生每天参加体育锻炼的时间作了一次抽样调查,其中部分结果记录如下:
时间分组(小时) | 频数(人数) | 频率 |
0≤t<0.5 | 10 | 0.2 |
0.5≤t<1 | 0.4 | |
1≤t<1.5 | 10 | 0.2 |
1.5≤t<2 | 0.1 | |
2≤t<2.5 | 5 | |
合计 | 1 |
请你将频数分布表和频数分布直方图补充完整.
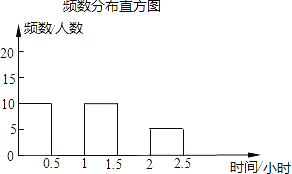
查看答案和解析>>
科目:初中数学 来源: 题型:
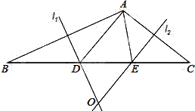
【题目】如图,在△ABC中,AB边的垂直平分线![]() 交BC于D,AC边的垂直平分线
交BC于D,AC边的垂直平分线![]() 交BC于E,
交BC于E, ![]() 与
与![]() 相交于点O,△ADE的周长为6cm.
相交于点O,△ADE的周长为6cm.
(1)求BC的长;
(2)分别连结OA、OB、OC,若△OBC的周长为16cm,求OA的长;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com