
【题目】如图,在△ABC中,∠ABC的平分线BF与△ABC的外角平分线CF相交于点F,过F作DF∥BC,交AB于D,交AC于E。

(1)写出图中所有的等腰三角形,并选择其中一个说明理由。
(2)直接写出BD,CE,DE之间的数量关系。
(3)若DE=5cm,CE=8cm,BF=24cm,求△BDF的面积。
【答案】(1)详见解析;(2)BD=DE+CE;(3)60.
【解析】试题分析:(1)根据已知条件,BF、CF分别平分∠ABC、∠ACB的外角,且DE∥BC,可得∴∠DBF=∠DFB,∠ECF=∠EFC,因此可判断出△BDF和△CEF为等腰三角形;
(2)由(1)可得出DF=BD,CE=EF,所以得BD-CE=DE;
(3)作BF边上的高,由勾股定理得到高为5,计算得到△BDF的面积为60.
试题解析:(1)△DBF、△ECF
以说明△DBF为例:
∵BF平分∠ABC
∴∠DBF=∠CBF
∵DF∥BC
∴∠CBF=∠DFB
∴∠DBF=∠DFB,
即△DBF为等腰三角形;
(2)存在:BDCE=DE,
证明:∵DF=BD,CE=EF,
∴BDCE=FDEF=DE.
(3)作DM⊥BF与点M,
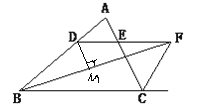
由(1)知△DBF为等腰三角形,
∴BM=![]() BF=12cm,
BF=12cm,
由(2)知BD=DE+EC=5+8=13cm,
由勾股定理,得DM=![]() =5cm,
=5cm,
S△BDF=![]() ×BF×DM=
×BF×DM=![]() ×24×5= 60(cm2)
×24×5= 60(cm2)


科目:初中数学 来源: 题型:
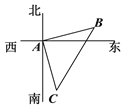
【题目】如图,在一次测绘活动中,某同学站在点A处观测停放于B、C两处的小船,测得船B在点A北偏东75°方向150米处,船C在点A南偏东15°方向120米处,则船B与船C之间的距离为______米(精确到0.1![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在△ABC的边AC上,要判定△ADB与△ABC相似,添加一个条件,不正确的是( )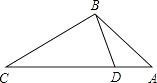
A.∠ABD=∠C
B.∠ADB=∠ABC
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD中,E、F分别是AB、AD边上的点,DE与CF交于点G.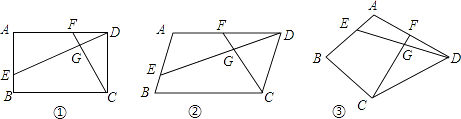
(1)如图①,若四边形ABCD是矩形,且DE⊥CF,求证:△ADE∽△DCF;
(2)如图②,若四边形ABCD是平行四边形,试探究:当∠B与∠EGC满足什么关系时, ![]() 成立?并证明你的结论;
成立?并证明你的结论;
(3)如图③,若BA=BC=6,DA=DC=8,∠BAD=90°,DE⊥CF,请直接写出 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b(k≠0)与反比例函数y= ![]() (m≠0)的图象有公共点A(1,a)、D(﹣2,﹣1).直线l与x轴垂直于点N(3,0),与一次函数和反比例函数的图象分别交于点B、C.
(m≠0)的图象有公共点A(1,a)、D(﹣2,﹣1).直线l与x轴垂直于点N(3,0),与一次函数和反比例函数的图象分别交于点B、C.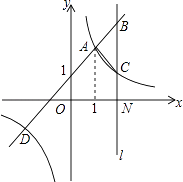
(1)求一次函数与反比例函数的解析式;
(2)根据图象回答,x在什么范围内,一次函数的值大于反比例函数的值;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从一个建筑物的A处测得对面楼BC的顶部B的仰角为32°,底部C的俯角为45°,观测点与楼的水平距离AD为31m,楼BC的高度大约为多少?(结果取整数).(参考数据:sin32°≈0.5,cos32°≈0.8,tan32°≈0.6)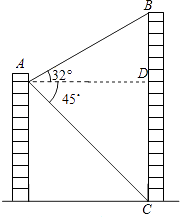
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间,某学校计划用彩色的地面砖铺设教学楼门前一块矩形操场ABCD的地面.已知这个矩形操场地面的长为100m,宽为80m,图案设计如图所示:操场的四角为小正方形,阴影部分为四个矩形,四个矩形的宽都为小正方形的边长,在实际铺设的过程总,阴影部分铺红色地面砖,其余部分铺灰色地面砖. 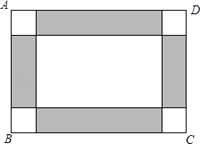
(1)如果操场上铺灰色地面砖的面积是铺红色地面砖面积的4倍,那么操场四角的每个小正方形边长是多少米?
(2)如果灰色地面砖的价格为每平方米30元,红色地面砖的价格为每平方米20元,学校现有15万元资金,问这些资金是否能购买所需的全部地面砖?如果能购买所学的全部地面砖,则剩余资金是多少元?如果不能购买所需的全部地面砖,教育局还应该至少给学校解决多少资金?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com