
分析 根据ai≠0(i=1,2,…,2016)满足$\frac{{|a}_{1}|}{{a}_{1}}$+$\frac{{|a}_{2}|}{{a}_{2}}$+…+$\frac{{|a}_{2016}|}{{a}_{2016}}$=1968,ai有24个是负数,1992个是正数,从而得到图象经过一、二、四象限的ai概率
解答 解:∵ai≠0(i=1,2,…,2016),且满足$\frac{{|a}_{1}|}{{a}_{1}}$+$\frac{{|a}_{2}|}{{a}_{2}}$+…+$\frac{{|a}_{2016}|}{{a}_{2016}}$=1968,
∴(2016-1968)÷2=24,2016-24=1992,
∴ai有24个是负数,1992个是正数,
∵ai<0时直线y=aix+i(i=1,2,…,2016)的图象经过一、二、四象限,
∴使直线y=aix+i(i=1,2,…,2016)的图象经过一、二、四象限的ai概率是$\frac{24}{2016}$=$\frac{3}{252}$=$\frac{1}{84}$,
故答案为:$\frac{1}{84}$.
点评 本题考查了概率的公式,将所有情况都列举出来是解决此题的关键.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:解答题
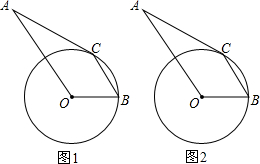 A为⊙O外一点,AC切⊙O于C,BC∥AO.
A为⊙O外一点,AC切⊙O于C,BC∥AO.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
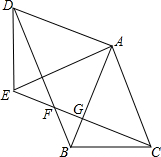 如图,在△ABC中,AB=AC=2,∠BAC=45°,△ABC绕点A顺时针旋转90°后得到△ADE,连接CE、BD、CE交BD于F,交AB于G.
如图,在△ABC中,AB=AC=2,∠BAC=45°,△ABC绕点A顺时针旋转90°后得到△ADE,连接CE、BD、CE交BD于F,交AB于G.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a<b<c<d | B. | b<a<c<d | C. | b<a<d<c | D. | a<b<d<c |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com