
| A.矩形 | B.菱形 | C.正方形 | D.等腰梯形 |
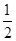 BD,EH=
BD,EH=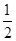 AC,推出EH∥FG,EF∥GH,EF⊥EH,EF=EH,根据正方形的判定定理推出即可.
AC,推出EH∥FG,EF∥GH,EF⊥EH,EF=EH,根据正方形的判定定理推出即可. ∵E、F、G、H分别是AD、AB、BC、CD的中点,
∵E、F、G、H分别是AD、AB、BC、CD的中点,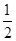 BD,EH=
BD,EH=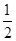 AC,
AC,

 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源:不详 题型:解答题
 (四个角都是直角,四边都相等,边长
(四个角都是直角,四边都相等,边长 的余料,修剪成如四边形
的余料,修剪成如四边形 的零件. 其中
的零件. 其中 ,
, 是
是 的中点.
的中点.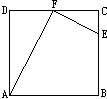
 的代数式表示
的代数式表示 的值;
的值; ,则△
,则△ 是直角三角形吗?为什么?
是直角三角形吗?为什么?查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 两动点M、N分别在边AB、AC上滑动,且MN∥BC,以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y(y >0),当x = ,公共部分面积y最大,y最大值 = ,
两动点M、N分别在边AB、AC上滑动,且MN∥BC,以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y(y >0),当x = ,公共部分面积y最大,y最大值 = ,
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 分米,CD=
分米,CD= 分米,梯形的高是
分米,梯形的高是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com