
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��l���ڵ�ֱ�ߵĽ���ʽΪy=![]() x����B����Ϊ��10��0����B��BC��ֱ��l������ΪC����P��ԭ�������x�᷽�����B�˶����ٶ�Ϊ1��λ/s��ͬʱ��Q�ӵ�B������B��C��ԭ�㷽���˶����ٶ�Ϊ2����λ/s����һ�����㵽���յ�ʱ����һ������Ҳ��ֹ֮ͣ�˶���
x����B����Ϊ��10��0����B��BC��ֱ��l������ΪC����P��ԭ�������x�᷽�����B�˶����ٶ�Ϊ1��λ/s��ͬʱ��Q�ӵ�B������B��C��ԭ�㷽���˶����ٶ�Ϊ2����λ/s����һ�����㵽���յ�ʱ����һ������Ҳ��ֹ֮ͣ�˶���

��1��OC= ��BC= ��
��2����t=5��s��ʱ������ֱ��PQ��ȷ��һ��M��ʹ��BCM���ܳ���С�����������Сֵ��
��3�����P���˶�ʱ��Ϊt��s������PBQ�����Ϊy������PBQ����ʱ����y��t�ĺ�����ϵʽ����д���Ա���t��ȡֵ��Χ��
���𰸡���1��8��6����2��16����3��y=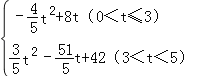 ��
��
��������
�����������1�����ݹ��ɶ������ɵô𰸣�
��2�������߶δ�ֱƽ���ߵ����ʣ��ɵ�ֱ��PQ�ϵĵ㵽O��C�ľ�����ȣ���������֮���߶���̣��ɵ�M����P���غϣ����������ε��ܳ����ɵô𰸣�
��3�������ٶ���ʱ��Ĺ�ϵ���ɵ�OP��BQ���������к������ɵ�QH�����������ε������ʽ���ɵô𰸣�
�⣺��1����ֱ��l���ڵ�ֱ�ߵĽ���ʽΪy=![]() x��BC��ֱ��l��
x��BC��ֱ��l��
��![]() =
=![]() ��
��
����OB=10��BC=3x��OC=4x��
����3x��2+��4x��2=102��
���x=2��x=��2���ᣩ��
OC=4x=8��BC=3x=6��
�ʴ�Ϊ��8��6��
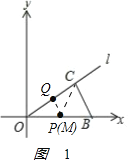
��2����ͼ1��
 ��
��
PQ��OC�Ĵ�ֱƽ���ߣ�OB��PQ��P��M����P���غϣ�
M��P���غ�ʱ��BCM���ܳ���С��
�ܳ���СΪ=BM+PM+BC=OB+BC=10+6=16��
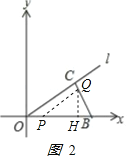
��3���ٵ�0��t��3ʱ����Q��QH��OB����ΪH����ͼ2��
 ��
��
PB=10��t��BQ=2t��HQ=2tsinB=2tcos��COB=2t��![]() =
=![]() t��
t��
y=![]() PBQH=
PBQH=![]() ��10��t��
��10��t��![]() t=��
t=��![]() t2+8t��
t2+8t��
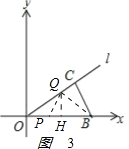
�ڵ�3��t��5ʱ����Q��QH��OB����ΪH����ͼ3��
 ��
��
PB=10��t��OQ=OC+BC��2t=14��2t��
QH=OQsin��QOH=��14��2t��![]() =
=![]() ��14��2t��=
��14��2t��=![]() ��
��![]() t��
t��
y=![]() PBQH=
PBQH=![]() ��10��t����
��10��t����![]() ��
��![]() t��=
t��=![]() t2��
t2��![]() t+42��
t+42��
��������y=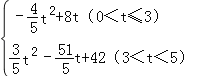 ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������У��Ǽ�������ǣ�����������
A. �Զ������ B. ͬ�ǵ�������
C. ���߶����˵���롡����������.�������߾�����ȵĵ㣬������ǵĽ�ƽ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ͼ������Խ��ߵĽ�����ʱ����ת90�㣬����ͼ��һ����ԭͼ���غϵ��ǣ�������
A. ƽ���ı��� B. ���� C. ���� D. ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��O�İ뾶Ϊ3��Բ��O��ֱ��L�ľ���Ϊ2����ֱ��L���O��λ�ù�ϵ��______________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ж���ʽ�˷�������ƽ���ʽ���м������( �������� )
A. (x+y)(��x��y) B. (2x+3y)(2x��3z) C. (��a��b)(a��b) D. (m��n)(n��m)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
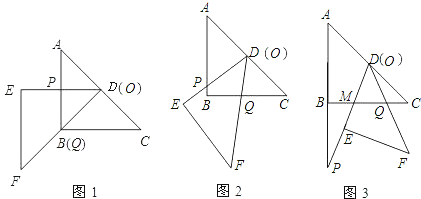
����Ŀ��������ȫ�ȵ�ֱ��������ABC��DEF������һ��ʹ���ǰ�DEF����Ƕ���D�����ǰ�ABC��б���е�O�غϣ�������ABC=��DEF=90������C=��F=45����AB=DE=4�������ǰ�ABC�̶������������ǰ�DEF�Ƶ�O��ת��������DE������AB�ཻ�ڵ�P������DF���߶�BC�ཻ�ڵ�Q��
��1����ͼ1��������DF������B������Q���B�غ�ʱ����֤��APD�ס�CDQ����ʱ��APCQ= ��
��2�������ǰ�DEF��ͼ1��ʾ��λ���Ƶ�O����ʱ�뷽����ת������ת��Ϊ��������0�㣼����90�㣬��APCQ��ֵ�Ƿ�ı䣿˵��������ɣ�
��3���ڣ�2���������£���CQ=x���������ǰ��ص����Ϊy����y��x�ĺ�����ϵʽ����ͼ2��ͼ3�������ã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���O������ԭ�㣬�ı���ABCO�����Σ���A������Ϊ��-3��4������C��x����������ϣ�ֱ��AC��y���ڵ�M��AB�߽�y���ڵ�H������BM��
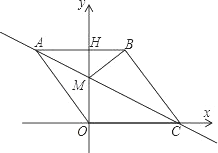
��1����ֱ��AC�Ľ���ʽ��
��2������P�ӵ�A������������ABC�ķ�����2����λ/����ٶ����յ�C�����˶�������PMB�����ΪS����P���˶�ʱ��Ϊt�룬��S��t֮��ĺ�����ϵʽ��Ҫ��д���Ա���t��ȡֵ��Χ����
��3������P�ӵ�A���������߶�AB������2����λ/����ٶ����յ�B�����˶�������MPB����BCO��Ϊ���ʱ����ȷ��t��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com