
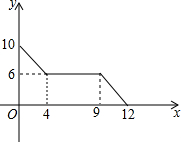
 如图,已知一对变量x,y满足图示中的函数关系.
如图,已知一对变量x,y满足图示中的函数关系.分析 (1)根据分段函数的图象,由自变量的取值范围分别写出各段函数的解析式即可;
(2)根据图象结合实际解答即可.
解答 解:(1)当0≤x≤4时,设函数解析式为y=kx+b,
把(0,10)和(4,6)代入可得:
$\left\{\begin{array}{l}{b=10}\\{4x+b=6}\end{array}\right.$,
解得:k=-1,b=10,
所以解析式为:y=-x+10(0≤x≤4);
当4<x≤9时,y=6;
当9<x≤12时,设函数解析式为y1=k1x+b1,
把(9,6)和(12,0)代入可得:
$\left\{\begin{array}{l}{9{k}_{1}+{b}_{1}=6}\\{12{k}_{1}+{b}_{1}=0}\end{array}\right.$,
解得:k1=-2,b1=24,
所以函数解析式为:y=-2x+24(9<x≤12);
综上所述,函数解析式为:$\left\{\begin{array}{l}{y=-x+10(0≤x≤4)}\\{y=6(4<x≤9)}\\{y=-2x+24(9<x≤12)}\end{array}\right.$;
(2)小明从离家10千米的A地出发回家,经过4小时以后达到距离家6千米的B地,在B地参观游玩5小时以后,继续赶路回家,终于在3小时以后回到家.其中x表示时间,y表示小明离家的距离.
点评 主要考查了用待定系数法求一次函数的解析式.先设y=kx+b,再结合图象把已知点的坐标代入可求出k,b的值,即得一次函数的解析式.


科目:初中数学 来源:2016-2017学年度海南省九年级第二次月考数学试卷(解析版) 题型:解答题
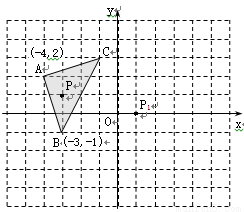
如图,△ABC中任意一点P(x0,y0)经过平移后对应点为P1(x0+4,y0-1).
(1)画出△ABC作同样的平移后得到的△A1B1C1,并写出A1、B1、C1的坐标.
(2)以点P1为位似中心,画出△A1B1C1的一个位似△A2B2C2,使它与△A1B1C1的相似比为2:1. 并写出A2、B2、C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 按要求作图并回答问题:
按要求作图并回答问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
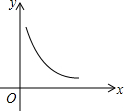 如图中的曲线是反比例函数y=$\frac{m+5}{x}$图象的一支,则m的取值范围是( )
如图中的曲线是反比例函数y=$\frac{m+5}{x}$图象的一支,则m的取值范围是( )| A. | m>-5 | B. | 0<m<5 | C. | -5<m<0 | D. | m<-5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 球 | 两红 | 一红一白 | 两白 |
| 礼金券(元) | 5 | 10 | 5 |
| 球 | 两红 | 一红一白 | 两白 |
| 礼金券(元) | 10 | 5 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,若双曲线y=$\frac{k}{x}$与边长为5的等边△AOB的边OA、AB分别相交于C、D两点,且OC=2BD.则实数k的值为4$\sqrt{3}$.
如图,若双曲线y=$\frac{k}{x}$与边长为5的等边△AOB的边OA、AB分别相交于C、D两点,且OC=2BD.则实数k的值为4$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com