
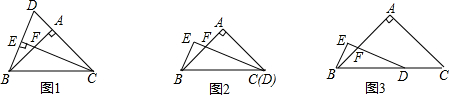
分析 (1)如图1,根据同角的余角相等证明∠DBA=∠DCF,利用ASA证明△AFC≌△ADB;
(2)①如图2,BE=$\frac{1}{2}$DF,作辅助线,构建全等三角形,证明△AGB≌△AFC,则BG=CF,再证明△CGE≌△CBE,可得结论;
②结论仍然成立,过点D做DP∥AC,交AB于点Q,交BE延长线于点P,证明△BQP≌△DQF,得BP=DF,再由等腰三角形三线合一的性质得:BE=$\frac{1}{2}$BP,即BE=$\frac{1}{2}$DF.
解答 证明:(1)如图1,∵BA⊥DC,
∴∠FAC=∠BAD=90°,
∴在Rt△ABD中,
∠D+∠DBA=90°,
同理∠D+∠DCF=90°,
∴∠DBA=∠DCF,
∵AB=AC,
∴△AFC≌△ADB(ASA);
(2)①解:BE=$\frac{1}{2}$DF,理由是: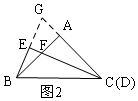
如图2,延长BE、DA交于G,
∵∠BAC=90°,
∴∠BAC=∠BAG=90°,
∴∠G+∠GBA=90°,
∵CE⊥BG,
∴∠CEG=90°,
∴∠G+∠ACF=90°,
∴∠GBA=∠ACF,
∵AB=AC,
∴△AGB≌△AFD,
∴BG=DF,
∵∠BEC=∠GEC=90°,
∠BCF=∠ACF,CE=CE,
∴△CGE≌△CBE,
∴BE=EG,
∴BE=$\frac{1}{2}$BG,
∴BE=$\frac{1}{2}$DF;
②成立,
证明:过点D做DP∥AC,交AB于点Q,交BE延长线于点P,
∵△ABC是等腰直角三角形,
∴∠ACB=45°,∠BAC=90°,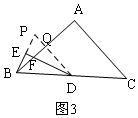
∵DP∥AC,
∴∠ACB=∠PDB=45°,
∠BQD=90°,
∴△QBD为等腰直角三角形,
即QB=QD,
∵∠BDE=$\frac{1}{2}$∠BCA=22.5°,
∴∠FDQ=22.5°,
∵BE⊥DF,
∴∠EBD=90°-22.5°=67.5°,
∠EPD=90°-22.5°=67.5°,
∴∠EBF=∠EBD-45°=22.5°,
在△BQP与△DQF中,
∵$\left\{\begin{array}{l}{∠BQP=∠DQF}\\{BQ=QD}\\{∠PBQ=∠FDQ}\end{array}\right.$,
∴△BQP≌△DQF(ASA),
∴BP=DF,
在△BDP中,
∵∠EPD=∠EBD,
∴△BDP是等腰三角形,
∵BE⊥DF,
∴BE=$\frac{1}{2}$BP,
即BE=$\frac{1}{2}$DF.
点评 本题是三角形的综合题,考查了全等三角形的性质和判定、等腰三角形的性质、等腰直角三角形的性质和判定,运用了类比的思想,作辅助线构建全等三角形是本题的关键,难度适中.


科目:初中数学 来源: 题型:选择题
| A. | x≠1 | B. | x$≠-\frac{5}{2}$ | C. | x$>-\frac{5}{2}$ | D. | x$<-\frac{5}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
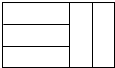 五个完全相同的小长方形拼成如图所示的大长方形,大长方形的周长是32cm,则小长方形的面积是( )
五个完全相同的小长方形拼成如图所示的大长方形,大长方形的周长是32cm,则小长方形的面积是( )| A. | 8cm2 | B. | 10cm2 | C. | 12cm2 | D. | 16cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
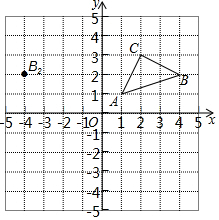 如图所示,在直角坐标系xOy中,△ABC三点的坐标分别为A(1,1),B(4,2),C(2,3).
如图所示,在直角坐标系xOy中,△ABC三点的坐标分别为A(1,1),B(4,2),C(2,3).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
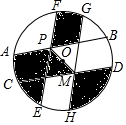 如图,一个半径为2cm的圆盘被分割成十个区域.其中,弦AB、CD关于圆心O对称,EF、GH关于圆心O对称,向盘中投掷一物体,则物体落在阴影部分的概率为$\frac{1}{2}$.
如图,一个半径为2cm的圆盘被分割成十个区域.其中,弦AB、CD关于圆心O对称,EF、GH关于圆心O对称,向盘中投掷一物体,则物体落在阴影部分的概率为$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com