
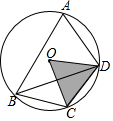
分析 (1)根据题意可得$\widehat{BD}$=2$\widehat{CD}$,进而可得∠BAD=∠COD,∠BAD=2∠CBD,再由条件∠CBD=30°可得∠BAD的度数;
(2)根据圆周角定理可得∠COD=60°,再根据扇形的面积公式可得答案.
解答 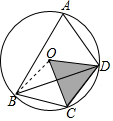 解:(1)∵C是为$\widehat{DB}$的中点,
解:(1)∵C是为$\widehat{DB}$的中点,
∴$\widehat{BD}$=2$\widehat{CD}$,
∴∠BAD=∠COD,
∵$\widehat{CD}$=$\widehat{CD}$,
∴∠COD=2∠CBD,
∴∠BAD=2∠CBD,
∵∠CBD=30°,
∴∠BAD=60°;
(2)∵$\widehat{CD}$=$\widehat{CD}$,
∴∠COD=2∠CBD,
∵∠CBD=30°,
∴∠COD=60°,
则S扇形OCD=$\frac{60×1{2}^{2}π}{360}$=24π.
点评 此题主要考查了圆周角定理,以及扇形的面积计算,关键是掌握在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,二次函数y=ax2+bx+c(a≠0)的图象,有下列4个结论:①abc>0;②b>a+c;③4a+2b+c>0;④b2-4ac>0;其中正确的是③④.
如图所示,二次函数y=ax2+bx+c(a≠0)的图象,有下列4个结论:①abc>0;②b>a+c;③4a+2b+c>0;④b2-4ac>0;其中正确的是③④.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1道 | B. | 2道 | C. | 3道 | D. | 4道 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com