
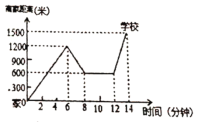
【题目】“珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明骑单车上学,当他骑了一段时间,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是 米,小明在书店停留了 分钟
(2)本次上学途中,小明一共行驶了 米,一共用了 分钟.
(3)我们认为骑单车的速度超过300米分钟就超越了安全限度.问:在整个上学的途中哪个时间段小明骑车速度最快,速度在安全限度内吗?
【答案】(1)1500,4;(2)2700,14;(3)12到14分钟时速度最快,不在安全限度内
【解析】
(1)由y轴表示路程,起点是家,终点是学校,即可得到小明家到学校的路程是1500米,根据与x轴平行的线段表示路程没有变化,观察图象分析其对应的时间即可;
(2)行驶的路程=家到学校的距离+2![]() 折回书店的路程,时间=到学校的时间-从家出发的时间;
折回书店的路程,时间=到学校的时间-从家出发的时间;
(3)根据每一时间段所行驶的路程及时间,分别计算各时间段的速度进行比较即可.
(1)∵y轴表示路程,起点是家,终点是学校,
∴小明家到学校的路程是1500米,
由图象可知:小明在书店停留12-8=4分钟,
故答案为:1500,4;
(2)本次上学途中,小明行驶的路程=1500+2![]() (1200-600)=2700(米),
(1200-600)=2700(米),
一共用的时间=14-0=14(分钟),
故答案为:2700,14;
(3)0到6分钟时,平均速度=![]() (米/分),
(米/分),
6到8分钟时,平均速度=![]() (米/分),
(米/分),
12到14分钟时,平均速度=![]() (米/分)
(米/分)
∴12到14分钟时速度最快,不在安全限度内.


科目:初中数学 来源: 题型:
【题目】七(1)班为“壮丽70年,奋斗新时代”演讲比赛购买A,B两种奖品.已知A奖品每件x元,B奖品每件y元.
⑴ 若购买A奖品m件,B奖品n件,共需要多少元;
⑵ 设购买A奖品m件,购买A,B两种奖品共10件:
① 购买两种奖品共需要多少元;
② 若购买A奖品至少2件,B奖品至少6件,请设计出购买方案,并说明每种方案的共需要多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知 AD 与 BC 相交于 E ,1 2 3, BD CD, ADB 90, CH AB于 H , CH 交 AD 于 F 。
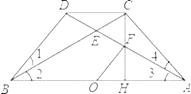
(1)求证: CD∥ AB ;
(2)求证: BDE ≌ ACE ;
(3)若O 为 AB 中点,求证:OF=![]() BE 。
BE 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人民商场准备购进甲、乙两种牛奶进行销售,若甲种牛奶的进价比乙种牛奶的进价每件少5元,其用90元购进甲种牛奶的数量与用100元购进乙种牛奶的数量相同.
(1)求甲种牛奶、乙种牛奶的进价分别是多少元?
(2)若该商场购进甲种牛奶的数量是乙种牛奶的3倍少5件,该商场甲种牛奶的销售价格为49元,乙种牛奶的销售价格为每件55元,则购进的甲、乙两种牛奶全部售出后,可使销售的总利润(利润=售价﹣进价)等于371元,请通过计算求出该商场购进甲、乙两种牛奶各自多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
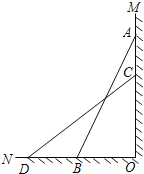
【题目】某研究性学习小组进行了探究活动.如图,已知一架竹梯AB斜靠在墙角MON处,竹梯AB=13m,梯子底端离墙角的距离BO=5m.
(1)求这个梯子顶端A距地面有多高;
(2)如果梯子的顶端A下滑4 m到点C,那么梯子的底部B在水平方向上滑动的距离BD=4 m吗?为什么?
(3)亮亮在活动中发现无论梯子怎么滑动,在滑动的过程中梯子上总有一个定点到墙角O的距离始终是不变的定值,会思考问题的你能说出这个点并说明其中的道理吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
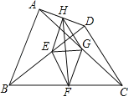
【题目】如图,E、F、G、H分别是BD、BC、AC、AD的中点,且AB=CD.结论:①EG⊥FH;②四边形EFGH是矩形;③HF平分∠EHG;④EG![]() BC;⑤四边形EFGH的周长等于2AB.其中正确的个数是( )
BC;⑤四边形EFGH的周长等于2AB.其中正确的个数是( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2013年四川广安8分)某商场筹集资金12.8万元,一次性购进空调、彩电共30台.根据市场需要,这些空调、彩电可以全部销售,全部销售后利润不少于1.5万元,其中空调、彩电的进价和售价见表格.
空调 | 彩电 | |
进价(元/台) | 5400 | 3500 |
售价(元/台) | 6100 | 3900 |
设商场计划购进空调x台,空调和彩电全部销售后商场获得的利润为y元.
(1)试写出y与x的函数关系式;
(2)商场有哪几种进货方案可供选择?
(3)选择哪种进货方案,商场获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,AC=8cm,BC=6cm,D、E分别为边AB、BC的中点,连结DE,点P从点A出发,沿折线AD﹣DE运动,到点E停止,点P在AD上以5cm/s的速度运动,在DE上以1cm/s的速度运动,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN.设点P的运动时间为t(s).
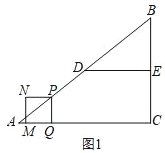
(1)当点P在线段DE上运动时,线段DP的长为_____cm.(用含t的代数式表示)
(2)当正方形PQMN与△ABC重叠部分图形为五边形时,设五边形的面积为S(cm2),求S与t的函数关系式,并写出t的取值范围.
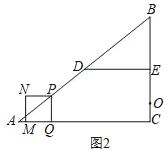
(3)如图2,若点O在线段BC上,且CO=1,以点O为圆心,1cm长为半径作圆,当点P开始运动时,⊙O的半径以0.2cm/s的速度开始不断增大,当⊙O与正方形PQMN的边所在直线相切时,求此时的t值.
查看答案和解析>>
科目:初中数学 来源: 题型:
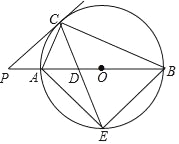
【题目】如图,AB是⊙O的直径,∠ACB的平分线交AB于点D,交⊙O于点E,过点C作⊙O的切线CP交BA的延长线于点P,连接AE.
(1)求证:PC=PD;
(2)若AC=5cm,BC=12cm,求线段AE,CE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com