练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，a＝4，b＝7，求阴影部分的面积（精确到0.01，圆周率取3.14）．

     


    解：阴影部分是一个矩形和两个四分之一个圆的面积之差．

    所以，阴影部分的面积

      S ＝（4＋7）×7－＝ 77

    ＝ 77  ＝ 77—  ＝ 25.975≈ 25.98.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：百分学生作业本课时3练1测七年级数学(下) 华东师大版 题型：022

    请阅读下面的材料：

    如图(1)所示，在等边三角形ABC中，AD是BC边上的中线，根据等腰三角形的“三线合一”性，AD平分∠BAC，且AD⊥BC，则有∠BAD＝30°，BD＝BC＝AB．于是可得出结论“直角三角形中，30°角所对的直角边等于斜边的一半”．

    请根据从上面材料中所得的信息解答下列问题：

    (1)

    在△ABC中，∠A∶∠B∶∠C＝1∶2∶3，CD⊥AB于D，AB＝a，则BD＝________．

    (2)

    如图(2)所示，在△ABC中，∠ACB＝90°，BC的垂直平分线交AB于D，垂足为E，当BD＝5 cm，∠B＝30°时，△ACD的周长＝________；

    (3)

    如图(3)所示，在△ABC中，AB＝AC，∠A＝120°，D是BC的中点，DE⊥AB，那么BE∶EA＝________．

    (4)

    如图(4)所示，在△ABC中，∠C＝90°，∠B＝15°，DM是AB的垂直平分线，BD＝8 cm，则AC＝________；

    (5)

    如图(5)所示，在等边三角形ABC中，D、E分别是BC、AC上的点，且∠1＝∠2，AD、BE交于点P，作BQ⊥AD于Q，猜想PB与PQ的数量关系，并简要说明理由．

    查看答案和解析>>

    科目：初中数学 来源：浙江省杭州市萧山义蓬片2011－2012学年七年级下学期能力测试数学试题 题型：044

    (1)阅读下面材料：点A、B在数轴上分别表示实数a、b，A、B两点之间的距离表示为|AB|．当A、B两点中有一点在原点时，不妨设点A在原点，如图1，|AB|＝|OB|＝|b|＝|a－b|当A、B两点都不在原点时，

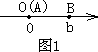
    ①如图2，点A、B都在原点的右边|AB|＝|OB|－|OA|＝|b|－|a|＝b－a＝|a－b|；

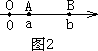
    ②如图3，点A、B都在原点的左边，|AB|＝|OB|－|OA|＝|b|－|a|＝b－a＝|a－b|；

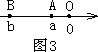
    ③如图4，点A、B在原点的两边，|AB|＝|OB|－|OA|＝|b|－|a|＝－b－(－a)＝|a－b|；综上，数轴上A、B两点之间的距离|AB|＝|a－b|．

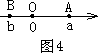
    (2)回答下列问题：

    ①数轴上表示2和5的两点之间的距离是________，数轴上表示－2和－5的两点之间的距离是________，

    数轴上表示1和－3的两点之间的距离是________；

    ②数轴上表示x和－1的两点A和B之间的距离是________，如果|AB|＝3，那么x________；

    ③当代数式|x＋2|十|x－5|取最小值时，相应的x的取值范围是________

    ④解方程∣x＋2∣＋∣x－5∣＝9

    查看答案和解析>>

    科目：初中数学 来源：北京市四中2011－2012学年七年级下学期期中考试数学试题 题型：047

    已知，如图，∠ABC＝∠ADC，BF、DE分别平分∠ABC与∠ADC，且∠1＝∠3．求证：AB∥DC．请根据条件进行推理，得出结论，并在括号内注明理由．

    证明：∵BF、DE分别平分∠ABC与∠ADC，

    ∴∠1＝∠ABC，∠2＝∠ADC．(________)

    ∵∠ABC＝∠ADC，

    ∵∠________＝∠________．

    ∵∠1＝∠3，

    ∴∠2＝________．(等量代换)

    ∴________∥________．(________)

    查看答案和解析>>

    科目：初中数学 来源：同步练习数学　　九年级上册 题型：044

    如图所示，AB是大圆的直径，分别把AB两等分、三等分、四等分、……、n等分，再分别以其中的一份为直径画圆，设大圆的周长为L，面积为S，那么，

    (1)当两等分AB时，小圆的周长＝________L，面积＝________S；

    (2)当三等分AB时，小圆的周长＝________L，面积＝________S；

    (3)当四等分AB时，小圆的周长＝________L，面积＝________S；

    (4)当n等分AB时，小圆的周长＝________L，面积＝________S(用含n的代数式表示)．

    查看答案和解析>>

    科目：初中数学 来源： 题型：单选题

    如图，∠1＝60º，∠2＝60º，∠3＝57º，则∠4＝57º，下面是A，B，C，D四个同学的推理过程，你认为推理正确的是（　　　）


    1. A.
      因为∠1＝60º＝∠2，所以a∥b，所以∠４＝∠3＝57º
    2. B.
      因为∠4＝57º＝∠3，所以a∥b，故∠1＝∠2＝60º
    3. C.
      因为∠2＝∠5，又∠1＝60º，∠2＝60º，故∠1＝∠5＝60º，所以a∥b，所以∠4＝∠3＝57º
    4. D.
      因为∠1＝60º，∠2＝60º，∠3＝57º，所以∠1＝∠3＝∠2-∠4＝60º-57º＝3º，

    查看答案和解析>>

    同步练习册答案