
阅读下面材料:
在学习小组活动中,小明探究了下面问题:菱形纸片ABCD的边长为2,折叠菱形纸片,将B、D两点重合在对角线BD上的同一点处,折痕分别为EF、GH.当重合点在对角线BD上移动时,六边形AEFCHG的周长的变化情况是怎样的?
小明发现:若∠ABC=60°,
①如图1,当重合点在菱形的对称中心O处时,六边形AEFCHG的周长为_________;
②如图2,当重合点在对角线BD上移动时,六边形AEFCHG的周长_________(填“改变”或“不变”).
请帮助小明解决下面问题:
如果菱形纸片ABCD边长仍为2,改变∠ABC的大小,折痕EF的长为m.
(1)如图3,若∠ABC=120°,则六边形AEFCHG的周长为_________;
(2)如图4,若∠ABC的大小为 ,则六边形AEFCHG的周长可表示为________.
,则六边形AEFCHG的周长可表示为________.




①6;②不变;(1) ;(2)
;(2) .
.
【解析】
试题分析:①根据折叠方法得到六边形AEFCHG是边长为2的正六边形,从而提出结论.
②根据相似三角形的判定和性质可得结论.
(1)当重合点在对角线BD上移动时,六边形AEFCHG的周长不变,与重合点在菱形的对称中心O处时相同,从而解三角形可得结论.
(2)同(1).
试题解析:①根据折叠方法得到六边形AEFCHG是边长为2的正六边形,从而提出结论.
②根据相似三角形的判定和性质可知当重合点在对角线BD上移动时,六边形AEFCHG的周长不变.
(1)由①②知,当重合点在对角线BD上移动时,六边形AEFCHG的周长不变,与重合点在菱形的对称中心O处时相同,故作出图形如图,可得AE=AH=CF=CG=1,EF=HG=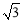 ,所以六边形AEFCHG的周长为
,所以六边形AEFCHG的周长为 .
.
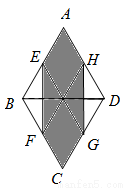
(2)同(1),可得AE=AH=CF=CG=1,EF=HG=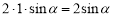 ,所以六边形AEFCHG的周长为
,所以六边形AEFCHG的周长为 .
.
考点:1.阅读理解和实践操作题;2.折叠对称的性质;3.菱形的性质;4.锐角三角函数定义;5.特殊角的三角函数值.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2013-2014学年北京市通州区中考二模数学试卷(解析版) 题型:解答题
列方程或方程组解应用题:
某停车场的收费标准如下:中型汽车的停车费为每辆6元,小型汽车的停车费为每辆4元. 现在停车场有中、小型汽车共50辆,这些车共缴纳停车费230元,问中、小型汽车各有多少辆?
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市燕山区中考一模数学试卷(解析版) 题型:选择题
2014年2月14日从北京航天飞行控制中心获悉,嫦娥二号卫星再次刷新我国深空探测最远距离记录,达到7 000万公里,这是我国航天器迄今为止飞行距离最远的一次“太空长征” .将7 000万用科学记数法表示应为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市海淀区中考一模数学试卷(解析版) 题型:解答题
列方程(组)解应用题:
某市计划建造80万套保障性住房,用于改善百姓的住房状况.开工后每年建造保障性住房的套数比原计划增加25%,结果提前两年保质保量地完成了任务.求原计划每年建造保障性住房多少万套?
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市朝阳区中考一模数学试卷(解析版) 题型:解答题
列方程或方程组解应用题:
从A地到B地有两条行车路线:
路线一:全程30千米,但路况不太好;
路线二:全程36千米,但路况比较好,一般情况下走路线二的平均车速是走路线一的
平均车速的1.8倍,走路线二所用的时间比走路线一所用的时间少20分钟.
那么走路线二的平均车速是每小时多少千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com