
ЁОЬтФПЁПШчЭМЫљЪОЃЌЖўДЮКЏЪ§![]() ЕФЭМЯѓгы
ЕФЭМЯѓгы![]() жсНЛгк
жсНЛгк![]() ЁЂ
ЁЂ![]() СНЕуЃЌгы
СНЕуЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌЦфжаЕу
ЃЌЦфжаЕу![]() дк
дк![]() жсЕФе§АыжсЩЯЃЌЕу
жсЕФе§АыжсЩЯЃЌЕу![]() дк
дк![]() жсЕФе§АыжсЩЯЃЌЯпЖЮ
жсЕФе§АыжсЩЯЃЌЯпЖЮ![]() ЁЂ
ЁЂ![]() ЕФГЄЃЈ
ЕФГЄЃЈ![]() ЃЉЪЧЗНГЬ
ЃЉЪЧЗНГЬ![]() ЕФСНИіИљЃЌЧв
ЕФСНИіИљЃЌЧв![]() ЕузјБъЮЊ
ЕузјБъЮЊ![]() ЃЎ
ЃЎ
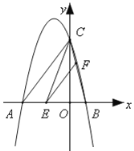
ЃЈ1ЃЉЧѓДЫЖўДЮКЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉШєЕу![]() ЪЧЯпЖЮ
ЪЧЯпЖЮ![]() ЩЯЕФвЛИіЖЏЕуЃЈгыЕу
ЩЯЕФвЛИіЖЏЕуЃЈгыЕу![]() ЁЂ
ЁЂ![]() ВЛжиКЯЃЉЃЌЙ§Еу
ВЛжиКЯЃЉЃЌЙ§Еу![]() зї
зї![]() ЁЮ
ЁЮ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() . Щш
. Щш![]() ЕФГЄЮЊ
ЕФГЄЮЊ![]() ЃЌЁї
ЃЌЁї![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌЧѓSгы
ЃЌЧѓSгы![]() жЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіздБфСП
жЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіздБфСП![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЛљДЁЩЯЪдЫЕУї![]() ЪЧЗёДцдкзюДѓжЕЃЌШєДцдкЃЌЧыЧѓГі
ЪЧЗёДцдкзюДѓжЕЃЌШєДцдкЃЌЧыЧѓГі![]() ЕФзюДѓжЕЃЌВЂЧѓГіДЫЪБЕу
ЕФзюДѓжЕЃЌВЂЧѓГіДЫЪБЕу![]() ЕФзјБъЃЌХаЖЯДЫЪБЁї
ЕФзјБъЃЌХаЖЯДЫЪБЁї![]() ЕФаЮзДЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФаЮзДЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() (0<m<8);ЃЈ3ЃЉЕБ
(0<m<8);ЃЈ3ЃЉЕБ![]() ЪБ
ЪБ![]() газюДѓжЕ
газюДѓжЕ![]() ЃЌДЫЪБЕу
ЃЌДЫЪБЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌЁї
ЃЌЁї![]() ЮЊЕШбќШ§НЧаЮ.
ЮЊЕШбќШ§НЧаЮ.
ЁОНтЮіЁП
ЃЈ1ЃЉЭЈЙ§НтЗНГЬx210xЃЋ16ЃН0ЕУЕНЖўДЮКЏЪ§ЭМЯѓЩЯЕФЕуBЁЂCЕФзјБъЃЌдйНсКЯAЕФзјБъЃЌРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉгУmБэЪіГіAEЁЂBEЕФГЄЃЌЕУЕНЁїBEFЁзЁїBACЃЌдйРћгУЯрЫЦШ§НЧаЮЕФаджЪЕУЕНБШР§ЪН![]() ЃЌЧѓГіEFЕФБэДяЪНЃЌРћгУsinЁЯFEGЃНsinЁЯCABЃН
ЃЌЧѓГіEFЕФБэДяЪНЃЌРћгУsinЁЯFEGЃНsinЁЯCABЃН![]() ЕУЕН
ЕУЕН![]() ЃЌЧѓГіFGЕФБэДяЪНЃЌдйИљОнSЃНSЁїBCESЁїBFEЧѓSгыmжЎМфЕФКЏЪ§ЙиЯЕЃЌmЕФжЕВЛГЌЙ§ABЕФГЄЃЎ
ЃЌЧѓГіFGЕФБэДяЪНЃЌдйИљОнSЃНSЁїBCESЁїBFEЧѓSгыmжЎМфЕФКЏЪ§ЙиЯЕЃЌmЕФжЕВЛГЌЙ§ABЕФГЄЃЎ
ЃЈ3ЃЉНЋSЃН![]() m2ЃЋ4ХфЗНЮЊSЃН
m2ЃЋ4ХфЗНЮЊSЃН![]() ЃЈm4ЃЉ2ЃЋ8ЃЌЧѓГіSЕФзюДѓжЕЃЌНјЖјХаЖЯГіДЫЪБЁїBCEЕФаЮзДЃЎ
ЃЈm4ЃЉ2ЃЋ8ЃЌЧѓГіSЕФзюДѓжЕЃЌНјЖјХаЖЯГіДЫЪБЁїBCEЕФаЮзДЃЎ
ЃЈ1ЃЉЗНГЬ![]() ЕФСНИіИљЮЊ2КЭ8.
ЕФСНИіИљЮЊ2КЭ8.
гЩгк![]() ЃЌЫљвд
ЃЌЫљвд![]() ЃЌ
ЃЌ![]() ЃЌЙЪ
ЃЌЙЪ![]() ЃЌЕу
ЃЌЕу![]() зјБъЮЊ
зјБъЮЊ![]() .
.
вђЮЊЕу![]() зјБъЮЊ
зјБъЮЊ![]() ЃЌЫљвд
ЃЌЫљвд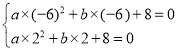 ЃЎ
ЃЎ
НтЕУ![]() ЃЌ
ЃЌ![]() .
.
ЙЪДЫЖўДЮКЏЪ§ЕФБэДяЪНЮЊ![]() .
.
ЃЈ2ЃЉЁпABЃН8ЃЌOCЃН8ЃЌвРЬтвтЃЌAEЃНmЃЌдђBEЃН8mЃЌ
ЁпOAЃН6ЃЌOCЃН8ЃЌ
ЁрACЃН10ЃЎ
ЁпEFЁЮACЃЌ
ЁрЁїBEFЁзЁїBACЃЎ
Ёр![]() ЃЎ
ЃЎ
МД![]() ЃЎ
ЃЎ
ЁрEFЃН![]() ЃЎ
ЃЎ
Й§ЕуFзїFGЁЭABЃЌДЙзуЮЊGЃЌдђsinЁЯFEGЃНsinЁЯCABЃН![]() ЃЎ
ЃЎ
Ёр![]() ЃЎ
ЃЎ
ЁрFGЃН![]()
![]() ЃН8mЃЎ
ЃН8mЃЎ
ЁрSЃНSЁїBCESЁїBFE
ЃН![]() ЃЈ8mЃЉЁС8
ЃЈ8mЃЉЁС8![]() ЃЈ8mЃЉЃЈ8mЃЉ
ЃЈ8mЃЉЃЈ8mЃЉ
ЃН![]() ЃЈ8mЃЉЃЈ88ЃЋmЃЉ
ЃЈ8mЃЉЃЈ88ЃЋmЃЉ
ЃН![]() ЃЈ8mЃЉm
ЃЈ8mЃЉm
ЃН![]() ЃЌздБфСПmЕФШЁжЕЗЖЮЇЪЧ0ЃМmЃМ8ЃЎ
ЃЌздБфСПmЕФШЁжЕЗЖЮЇЪЧ0ЃМmЃМ8ЃЎ
ЃЈ3ЃЉДцдкЃЎ
РэгЩШчЯТЃК
ЁпSЃН![]() =
=![]() ЃЈm4ЃЉ2ЃЋ8ЃЌЧв
ЃЈm4ЃЉ2ЃЋ8ЃЌЧв![]() ЃМ0ЃЌ
ЃМ0ЃЌ
ЁрЕБmЃН4ЪБЃЌSгазюДѓжЕЃЌSзюДѓжЕЃН8ЃЎ
ЁпmЃН4ЃЌ
ЁрЕуEЕФзјБъЮЊЃЈ2ЃЌ0ЃЉЃЎ
ЁрЁїBCEЮЊЕШбќШ§НЧаЮЃЎ


 аЁбЇПЮЪБзївЕШЋЭЈСЗАИЯЕСаД№АИ
аЁбЇПЮЪБзївЕШЋЭЈСЗАИЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§yЃНx2Љ4x+3ЃЎ
ЃЈ1ЃЉгУХфЗНЗЈНЋyЃНx2Љ4x+3ЛЏГЩyЃНaЃЈxЉhЃЉ2+kЕФаЮЪНЃЛ
ЃЈ2ЃЉдкЦНУцжБНЧзјБъЯЕжаЃЌЛГіетИіЖўДЮКЏЪ§ЕФЭМЯѓЃЛ
ЃЈ3ЃЉаДГіЕБxЮЊКЮжЕЪБЃЌyЃО0ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
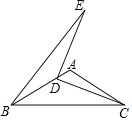
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌABЃНACЃЌЁЯBACЃН120ЁуЃЌЕуDЮЊABБпЩЯвЛЕуЃЈВЛгыЕуBжиКЯЃЉЃЌСЌНгCDЃЌНЋЯпЖЮCDШЦЕуDФцЪБеыа§зЊ90ЁуЃЌЕуCЕФЖдгІЕуЮЊEЃЌСЌНгBEЃЎШєABЃН2ЃЌдђЁїBDEУцЛ§ЕФзюДѓжЕЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЙигкxЕФЗНГЬkx2Љ3x+1ЃН0гаЪЕЪ§ИљЃЎ
(1)ЧѓkЕФШЁжЕЗЖЮЇЃЛ
(2)ШєИУЗНГЬгаСНИіЪЕЪ§ИљЃЌЗжБ№ЮЊx1КЭx2ЃЌЕБx1+x2+x1x2ЃН4ЪБЃЌЧѓkЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
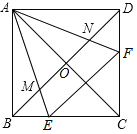
ЁОЬтФПЁПШчЭМЃЌЕуEЃЌFЗжБ№ЮЊе§ЗНаЮABCDЕФБпBCЃЌCDЩЯвЛЕуЃЌACЃЌBDНЛгкЕуOЃЌЧвЁЯEAF=45ЁуЃЌAEЃЌAFЗжБ№НЛЖдНЧЯпBDгкЕуMЃЌNЃЌдђгавдЯТНсТлЃКЂйЁЯAEB=ЁЯAEF=ЁЯANMЃЛЂкEF=BE+DFЃЛЂлЁїAOMЁзЁїADFЃЛЂмSЁїAEF=2SЁїAMNЃЌвдЩЯНсТлжаЃЌе§ШЗЕФЪЧ______ .ЃЈЧыАбе§ШЗНсТлЕФађКХЖМЬюЩЯЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпгыxжсНЛгкAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉСНЕуЃЌгыyжсНЛгкЕуCЃЈ0ЃЌ3ЃЉ.
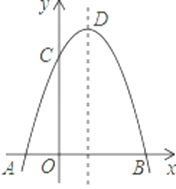
ЃЈ1ЃЉЧѓДЫХзЮяЯпЫљЖдгІКЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉШєM ЪЧХзЮяЯпЖдГЦжсЩЯвЛИіЖЏЕуЃЌЧѓЕБ MA+MC ЕФжЕзюаЁЪБ M ЕузјБъЃЛ
ЃЈ3ЃЉШєХзЮяЯпЕФЖЅЕуЮЊDЃЌдкЦфЖдГЦжсгвВрЕФХзЮяЯпЩЯЪЧЗёДцдкЕуPЃЌЪЙЕУЁїPCDЮЊЕШбќШ§НЧаЮЃПШєДцдкЃЌЧѓГіЗћКЯЬѕМўЕФЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙигкxЕФКЏЪ§y=ax2+(2a+1)x+a-1гызјБъжсгаСНИіНЛЕуЃЌдђaЕФШЁжЕгаЃЈ ЃЉ
A.1ИіB.2ИіC.3ИіD.4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвЪаВшвЖзЈТєЕъЯњЪлФГЦЗХЦВшвЖЃЌЦфНјМлЮЊУПЧЇПЫ 240 дЊЃЌАДУПЧЇПЫ 400 дЊГіЪлЃЌЦНОљУПжмПЩЪлГі 200 ЧЇПЫЃЌКѓРДОЙ§ЪаГЁЕїВщЗЂЯжЃЌЕЅМлУПНЕЕЭ 10 дЊЃЌдђЦНОљУПжмЕФЯњЪлСППЩдіМг 40 ЧЇПЫЃЌШєИУзЈТєЕъЯњЪлетжжЦЗХЦВшвЖвЊЯыЦНОљУПжмЛёРћ 41600 дЊЃЌЧыЛиД№ЃК
ЃЈ1ЃЉУПЧЇПЫВшвЖгІНЕМлЖрЩйдЊЃП
ЃЈ2ЃЉдкЦНОљУПжмЛёРћВЛБфЕФЧщПіЯТЃЌЮЊОЁПЩФмШУРћгкЙЫПЭЃЌгЎЕУЪаГЁЃЌИУЕъгІАДдЪлМлЕФ МИелГіЪлЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвУЧЖЈвхСНИіВЛЯрНЛЕФКЏЪ§ЭМЯѓдкЪњжБЗНЯђЩЯЕФзюЖЬОрРыЮЊетСНИіКЏЪ§ЕФЁАКЭаГжЕЁБЃЎ
(1)ЧѓХзЮяЯпyЃНx2Љ2x+2гыxжсЕФЁАКЭаГжЕЁБЃЛ
(2)ЧѓХзЮяЯпyЃНx2Љ2x+2гыжБЯпyЃНxЉ1ЕФЁАКЭаГжЕЁБЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com