
如图,M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B=α,且DM交AC于F,ME交BC于G.

(1)写出图中三对相似三角形,并证明其中的一对;
(2)连结FG,如果α=45°,AB=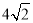 ,AF=3,求FC和FG的长.
,AF=3,求FC和FG的长.
(1)△AME∽△MFE,△BMD∽△MGD,△AMF∽△BGM,(2)1,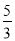 .
.
【解析】
试题分析:(1)根据已知条件,∠DME=∠A=∠B=α,结合图形上的公共角,即可推出△DMG∽△DBM,△EMF∽△EAM,AMF∽△BGM;
(2)根据相似三角形的性质,推出BG的长度,依据锐角三角函数推出AC的长度,即可求出CG、CF的长度,继而推出FG的长度.
试题解析:(1)△AME∽△MFE,△BMD∽△MGD,△AMF∽△BGM,
∵∠AMD=∠B+∠D,∠BGM=∠DMG+∠D
又∠B=∠A=∠DME=α
∴∠AMF=∠BGM,
∴△AMF∽△BGM,
(2)连接FG,
由(1)知,△AMF∽△BGM,
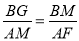 ,
,
BG=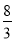
∠α=45°,
∴△ABC为等腰直角三角形,
∵M是线段AB中点,
∴AB=4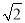 ,AM=BM=2
,AM=BM=2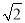 ,
,
AC=BC=4,CF=AC-AF=1,
CG=4-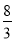 =
=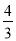 ,
,
∴由勾股定理得FG=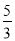
考点:相似三角形的判定.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源:2014-2015学年浙江省温州市五校联赛九年级实验B班1月联考数学试卷(解析版) 题型:填空题
如图,△ABC中,CD⊥AB于D,E是AC的中点.若AD=6,DE=5,则CD的长等于 .

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省张家港市九年级上学期第三次阶段性测试数学试卷(解析版) 题型:计算题
(本题满分8分)如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
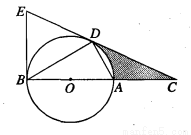
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为1,∠CBD=30°,则图中阴影部分的面积;
(3)过点B作⊙O的切线交CD的延长线于点E若BC=12,tan∠CDA=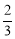 ,求BE的长.
,求BE的长.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省张家港市九年级上学期第三次阶段性测试数学试卷(解析版) 题型:选择题
已知两点(-2,y1)(3,y2)均在抛物线y=ax2+bx+c上,点C(x0,y0)是该抛物线的顶点,若y1<y2≤y0,则x0的取值范围是( )
A.x0>3 B.x0>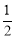 C.-2<x0<3 D.-1<x0<
C.-2<x0<3 D.-1<x0<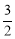
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省张家港市九年级上学期第三次阶段性测试数学试卷(解析版) 题型:选择题
用配方法解方程x2-2x-1=0时,配方后得的方程为( )
A.(x+1)2=0 B.(x-1)2=0
C.(x+1)2=2 D.(x-1)2=2
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省苏州市九年级12月月考数学试卷(解析版) 题型:选择题
已知下列函数①y=x2 ②y=-x2 ③y=(x-1)2+2,其中,图象通过平移可以得到函数y=x2+2x-3的图像的有( )
A.①、② B.①、③ C.②、③ D.①、②、③
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级12月阶段调研测试数学试卷(解析版) 题型:解答题
(本题满分10分)如图的⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,并与AB延长线交于点E.
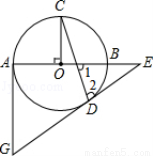
(1)求证:∠1=∠2.
(2)已知:OF:OB=1:3,⊙O的半径为3,求AG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com