
(本题满分10分)如图的⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,并与AB延长线交于点E.
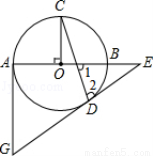
(1)求证:∠1=∠2.
(2)已知:OF:OB=1:3,⊙O的半径为3,求AG的长.
见解析
【解析】
试题分析:(1)连接OD,因为DE为⊙O的切线,所以OD⊥DE,又OC⊥OB,然后根据互余的关系可证∠1=∠2;(2)由(1)中∠1=∠2可得EF=ED,设DE=x,在Rt△ODE中,由勾股定理求得x =4,然后证Rt△EOD∽Rt△EGA.可求出AG的长.
试题解析:(1)证明:如图,连接OD,
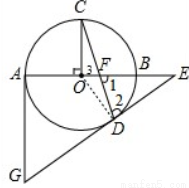
∵DE为⊙O的切线,∴OD⊥DE.∴∠ODE=90°,即∠2 ∠ODC=90°,∵OC=OD,∴∠C=∠ODC.∴∠2 ∠C=90°.∵OC⊥OB,∴∠C ∠3=90°.∴∠2=∠3,∵∠1=∠3,∴∠1=∠2.
(2)∵OF:OB=1:3,⊙O的半径为3,∴OF=1.∵∠1=∠2,∴EF=ED,在Rt△ODE中,OD=3,设DE=x,则EF=x,OE=1+x,所以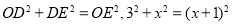 ,解得x =4.∴DE=4,OE=5.
,解得x =4.∴DE=4,OE=5.
∵AG为⊙O的切线,∴AG⊥AE.∴∠GAE=90°.∴∠ODE=∠GAE,∵∠OED=∠GEA,∴Rt△EOD∽Rt△EGA.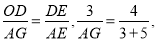 解得AG=6.
解得AG=6.
考点:1.切线的性质;2.等腰三角形的判定和性质;3.勾股定理;4.相似三角形的判定和性质.


科目:初中数学 来源:2014-2015学年浙江省台州市九年级上学期期中考试数学试卷(解析版) 题型:填空题
已知反比例函数y=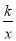 的图象经过点(1,-2),则k=__________.
的图象经过点(1,-2),则k=__________.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省苏州市九年级12月月考数学试卷(解析版) 题型:解答题
如图,M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B=α,且DM交AC于F,ME交BC于G.

(1)写出图中三对相似三角形,并证明其中的一对;
(2)连结FG,如果α=45°,AB=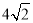 ,AF=3,求FC和FG的长.
,AF=3,求FC和FG的长.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级12月阶段调研测试数学试卷(解析版) 题型:填空题
已知圆锥的底面半径是3cm,母线长是5cm,则圆锥的侧面积是 __cm2.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广西省九年级12月月考数学试卷(解析版) 题型:解答题
如图,将一把两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心 ,另一边所在直线与半圆相交于点
,另一边所在直线与半圆相交于点 ,量出半径
,量出半径 ,弦
,弦 ,求这把直尺的宽度.
,求这把直尺的宽度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com