
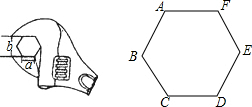
 如图,要打开一个边长a=12mm的六角形螺帽(下图的正六边形ABCDEF是六角形螺帽的放大图),扳手张开的开口b至少要多少??
如图,要打开一个边长a=12mm的六角形螺帽(下图的正六边形ABCDEF是六角形螺帽的放大图),扳手张开的开口b至少要多少?? 分析 根据题意,即是求该正六边形的边心距的2倍.构造一个由半径、半边、边心距组成的直角三角形,且其半边所对的角是30度,再根据锐角三角函数的知识求解即可.
解答 解:设正多边形的中心是O,其一边是AB,
∴∠AOB=∠BOC=60°,
∴OA=OB=AB=OC=BC,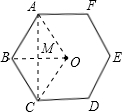
∴四边形ABCO是菱形,
∵AB=12mm,∠AOB=60°,
∴cos∠BAC=$\frac{AM}{AB}$,
∴AM=12×$\frac{\sqrt{3}}{2}$=6$\sqrt{3}$,
∵OA=OC,且∠AOB=∠BOC,
∴AM=MC=$\frac{1}{2}$AC,
∴AC=2AM=12$\sqrt{3}$mm.
即扳手张开的开口b至少要12$\sqrt{3}$mm.
点评 本题考查了正多边形和圆的知识,构造一个由半径、半边、边心距组成的直角三角形,熟练运用锐角三角函数进行求解是解题的关键.


科目:初中数学 来源: 题型:解答题
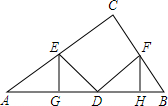 如图,Rt△ABC中,∠C=90°,D点是AB的中点,E、F分别是AC、BC上的两个动点,DE⊥DF,EG⊥AB于G,FH⊥AB于H.
如图,Rt△ABC中,∠C=90°,D点是AB的中点,E、F分别是AC、BC上的两个动点,DE⊥DF,EG⊥AB于G,FH⊥AB于H.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com