
【题目】如图,直线y=﹣ ![]() x+4交x轴于点A,交y轴于点C,抛物线y=ax2﹣
x+4交x轴于点A,交y轴于点C,抛物线y=ax2﹣ ![]() x+c过点A,交y轴于点B(0,﹣2)
x+c过点A,交y轴于点B(0,﹣2)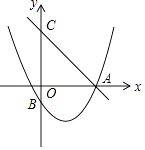
(1)求抛物线的解析式;
(2)点M为抛物线在第四象限部分上的一个动点,求四边形BMAC面积的最大值;
(3)点D为抛物线对称轴上一点,规定:d=|AD﹣BD|,探究d是否存在最大值?若存在,请直接写出d的最大值及此时点D的坐标.
【答案】
(1)
解:∵直线y=﹣ ![]() x+4交x轴于点A,交y轴于点C,
x+4交x轴于点A,交y轴于点C,
∴点A坐标为(3,0)、点C坐标为(0,4),
∵抛物线y=ax2﹣ ![]() x+c过点A,交y轴于点B(0,﹣2).
x+c过点A,交y轴于点B(0,﹣2).
∴ ![]() ,解得:
,解得: 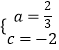 ,
,
∴抛物线解析式为y= ![]() x2﹣
x2﹣ ![]() x﹣2;
x﹣2;
(2)
解:如图1所示,过点M作x轴的垂线,交直线y=﹣ ![]() x+4于点N.
x+4于点N.
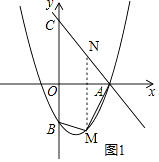
设点M(x, ![]() x2﹣
x2﹣ ![]() x﹣2),则点N的坐标为(x,﹣
x﹣2),则点N的坐标为(x,﹣ ![]() x+4).
x+4).
∵MN∥BC,
∴MN和BC间的距离为x,MN=(﹣ ![]() x+4)﹣(
x+4)﹣( ![]() x2﹣
x2﹣ ![]() x﹣2)=6﹣
x﹣2)=6﹣ ![]() x2,点A到MN的距离d=3﹣x,则四边形BMNC的面积S1=
x2,点A到MN的距离d=3﹣x,则四边形BMNC的面积S1= ![]() (BC+MN)x=6x﹣
(BC+MN)x=6x﹣ ![]() x3,
x3,
△ANM的面积S2= ![]() MN(3﹣x)=
MN(3﹣x)= ![]() x3﹣x2﹣3x+9,
x3﹣x2﹣3x+9,
∴四边形BMAC的面积S=S1+S2=6x﹣ ![]() x3+
x3+ ![]() x3﹣x2﹣3x+9=﹣x2+3x+9=﹣(x﹣
x3﹣x2﹣3x+9=﹣x2+3x+9=﹣(x﹣ ![]() )2+
)2+ ![]() ,
,
∵0<x<3,
∴当x= ![]() 时,四边形BMAC面积的最大值为
时,四边形BMAC面积的最大值为 ![]() .
.
(3)
解:如图2所示:记抛物线与x轴的另一个交点为E.
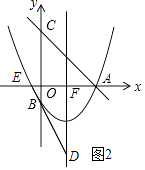
∵抛物线的对称为x=﹣ ![]() =1,A(3,0),
=1,A(3,0),
∴E(﹣1,0).
∴OE=1,EF=2.
∵点E与点A关于抛物线的对称轴对称,
∴ED=AD.
∴d=|AD﹣BD|=|ED﹣BD|.
∵当点E、B、D不在同一条直线上时,d=|ED﹣BD|<BE,当点E、B、D在同一条直线上时,d=|ED﹣BD|=BE,
∴d的最大值=BE= ![]() =
= ![]() .
.
∵OB∥DF,
∴△EOB∽△EFD.
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,解得:DF=4.
,解得:DF=4.
∴D(1,﹣4).
【解析】(1)根据直线与坐标轴的交点得出点A、C坐标,再根据待定系数法求得抛物线解析式;(2)设点M(x, ![]() x2﹣
x2﹣ ![]() x﹣2),过点M作x轴的垂线,交直线y=﹣
x﹣2),过点M作x轴的垂线,交直线y=﹣ ![]() x+4于点N,先求出四边形BMNC的面积S1=
x+4于点N,先求出四边形BMNC的面积S1= ![]() (BC+MN)x=6x﹣
(BC+MN)x=6x﹣ ![]() x3 , △ANM的面积S2=
x3 , △ANM的面积S2= ![]() MN(3﹣x)=
MN(3﹣x)= ![]() x3﹣x2﹣3x+9,根据四边形BMAC的面积S=S1+S2得到四边形的面积与x的函数关系式,然后利用配方法求解即可;(3)记抛物线与x轴的另一个交点为E,抛物线的对称轴与x轴的交点为F,当点E、B、D在同一条直线上时,d有最大值,然后证明△EOB∽△EFD,依据相似三角形的性质可求得DF的长,从而可得到点D的坐标.
x3﹣x2﹣3x+9,根据四边形BMAC的面积S=S1+S2得到四边形的面积与x的函数关系式,然后利用配方法求解即可;(3)记抛物线与x轴的另一个交点为E,抛物线的对称轴与x轴的交点为F,当点E、B、D在同一条直线上时,d有最大值,然后证明△EOB∽△EFD,依据相似三角形的性质可求得DF的长,从而可得到点D的坐标.
【考点精析】掌握二次函数的图象和二次函数的性质是解答本题的根本,需要知道二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


科目:初中数学 来源: 题型:
【题目】为了测量出大楼AB的高度,从距离楼底B处50米的点C(点C与楼底B在同一水平面上)出发,沿倾斜角为30°的斜坡CD前进20米到达点D,在点D处测得楼顶A的仰角为64°,求大楼AB的高度(结果精确到1米)(参考数据:sin64°≈0.9,cos64°≈0.4,tan64°≈2.1, ![]() ≈1.7)
≈1.7)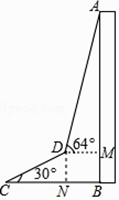
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)分别求出代数式a2﹣2ab+b2和(a﹣b)2的值.
①其中a=![]() ,b=3;②a=5,b=3;③a=﹣1,b=2.
,b=3;②a=5,b=3;③a=﹣1,b=2.
(2)观察(1)中的①②③你发现这两个多项式有什么关系,直接写出.
(3)利用你发现的规律,求出1.4372﹣2×1.437×0.437+0.4372的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列计算:
(1)78-23÷70=70÷70=1;
(2)12-7×(-4)+8÷(-2)=12+28-4=36;
(3)12÷(2×3)=12÷2×3=6×3=18;
(4)32×3.14+3×(-9.42)=3×9.42+3×(-9.42)=0.
其中错误的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
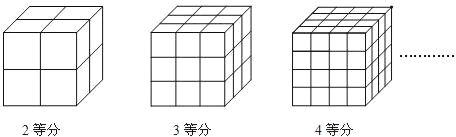
【题目】将一个正方体的表面全涂上颜色.
(1)如果把正方体的棱2等分,然后沿等分线把正方体切开,能够得到8个小正方体,设其中3面被涂上颜色的有a个,则a= ;
(2)如果把正方体的棱三等分,然后沿等分线把正方体切开,能够得到27个小正方体.设这些小正方体中有3个面涂有颜色的有a个,各个面都没有涂色的有b个,则a+b= ;
(3)如果把正方体的棱4等分,然后沿等分线把正方体切开,能够得到64个小正方体.设这些小正方体中有2个面涂有颜色的有c个,各个面都没有涂色的有b个,则c+b= ;
(4)如果把正方体的棱n等分,然后沿等分线把正方体切开,能够得到 个小正方体.设这些小正方体中有2个面涂有颜色的有c个,各个面都没有涂色的有b个,则c+b= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.
请解决下列问题:
(1)已知点M,N是线段AB的勾股分割点,且BN>MN>AM.若AM=2,MN=3,求BN的长;
(2)如图2,若点F、M、N、G分别是AB、AD、AE、AC边上的中点,点D,E是线段BC的勾股分割点,且EC>DE>BD,求证:点M,N是线段FG的勾股分割点.

查看答案和解析>>
科目:初中数学 来源: 题型:
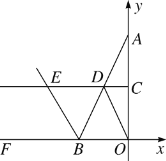
【题目】如图,在平面直角坐标系中,已知点A(0,6),B(b,0),且b<0,C,D分别是OA,AB的中点,△AOB的外角∠DBF的平分线BE与CD的延长线交于点E.
(1)求证:∠DAO=∠DOA;
(2)①若b=-8,求CE的长;
②若CE=![]() +1,则b=________;
+1,则b=________;
(3)是否存在这样的b值,使得四边形OBED为平行四边形?若存在,请求出此时四边形OBED对角线的交点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
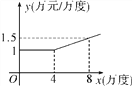
【题目】某工厂在生产过程中每消耗1万度电可以产生产值5.5万元,电力公司规定,该工厂每月用电量不得超过16万度;月用电量不超过4万度时,单价都是1万元/万度;超过4万度时,超过部分电量单价将按用电量进行调整.电价y与月用电量x的函数关系可以用下图来表示(效益=产值-用电量×电价).
(1)求y与月用电量x之间的函数关系式,并写出自变量的取值范围;
(2)设工厂的月效益为z(万元),写出z与用电量x之间的函数关系式;
(3)求工厂最大月效益.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PB切⊙O于点B,联结PO并延长交⊙O于点E,过点B作BA⊥PE交⊙O于点A,联结AP,AE. 
(1)求证:PA是⊙O的切线;
(2)如果OD=3,tan∠AEP= ![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com