
【题目】为了测量出大楼AB的高度,从距离楼底B处50米的点C(点C与楼底B在同一水平面上)出发,沿倾斜角为30°的斜坡CD前进20米到达点D,在点D处测得楼顶A的仰角为64°,求大楼AB的高度(结果精确到1米)(参考数据:sin64°≈0.9,cos64°≈0.4,tan64°≈2.1, ![]() ≈1.7)
≈1.7)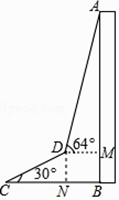
【答案】解:在Rt△CDN中,∵CD=20米,∠C=30°,
∴BM=DN= ![]() CD=10米,CN=CDcos∠C=20×
CD=10米,CN=CDcos∠C=20× ![]() =10
=10 ![]() 米,
米,
∵BC=50米,
∴DM=BN=BC﹣CN=50﹣10 ![]() ,
,
在Rt△ADN中,由tan∠ADN= ![]() 可得AM=DMtan∠ADN=(50﹣10
可得AM=DMtan∠ADN=(50﹣10 ![]() )tan64°,
)tan64°,
则AB=AM+BM=(50﹣10 ![]() )tan64°+10≈79米,
)tan64°+10≈79米,
答:楼AB的高度约为79米.
【解析】在Rt△CDN中求得BM=DN= ![]() CD=10、CN=CDcos∠C=10
CD=10、CN=CDcos∠C=10 ![]() ,即可知DM=BN=50﹣10
,即可知DM=BN=50﹣10 ![]() ,根据AB=BM+AM=BM+DMtan∠ADN可得答案.
,根据AB=BM+AM=BM+DMtan∠ADN可得答案.
【考点精析】通过灵活运用关于仰角俯角问题,掌握仰角:视线在水平线上方的角;俯角:视线在水平线下方的角即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图所示,△ABC中,∠A=90°,D是AC上一点,且∠ADB=2∠C,P是BC上任一点,PE⊥BD于点E,PF⊥AC于点F,下列结论:
①△DBC是等腰三角形;②∠C=30°;③PE+PF=AB;④PE2+AF2=BP2.
其中结论正确的个数是( )
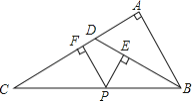
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一慢车和一快车沿相同路线从A地到B地,所行的路程与时间的函数图象如图所示.请你根据图象,回答下列问题: 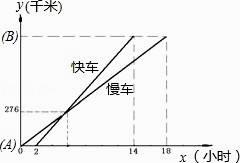
(1)慢车比快车早出发小时,快车追上慢车时行驶了千米,快车比慢车早小时到达B地;
(2)在下列3个问题中任选一题求解(多做不加分): ①快车追上慢车需几个小时?
②求慢车、快车的速度;
③求A、B两地之间的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
(1)【阅读发现】如图①,在△ABC中,∠ACB=45°,AD⊥BC于点D,E为AD上一点,且DE=BD,可知AB=CE.
(2)【类比探究】如图②,在正方形ABCD中,对角线AC与BD交于点O,E是OC上任意一点,AG⊥BE于点G,交BD于点F.判断AF与BE的数量关系,并加以证明.
(3)【推广应用】在图②中,若AB=4,BF= ![]() ,则△AGE的面积为 .
,则△AGE的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC,过AD的中点O作EF⊥AD,分别交AB、AC于点E、F,连接DE、DF. 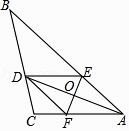
(1)判断四边形AFDE是什么四边形?请说明理由;
(2)若BD=8,CD=3,AE=4,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
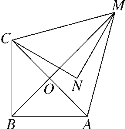
【题目】(题文)如图,在等腰直角三角形MNC中,CN=MN=![]() ,将△MNC绕点C顺时针旋转60°,得到△ABC,连接AM,BM,BM交AC于点O.
,将△MNC绕点C顺时针旋转60°,得到△ABC,连接AM,BM,BM交AC于点O.
(1)∠NCO的度数为________;
(2)求证:△CAM为等边三角形;
(3)连接AN,求线段AN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
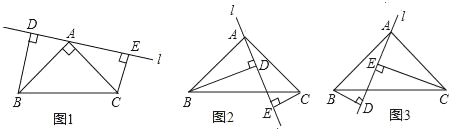
【题目】在△ABC中,∠BAC=90°,AB=AC,l是过A的一条直线,BD⊥AE于D,CE⊥AE于E.求证:
(1)当直线l绕点A旋转到如图1位置时,试说明:DE=BD+CE.
(2)若直线l绕点A旋转到如图2位置时,试说明:DE=BD﹣CE.
(3)若直线l绕点A旋转到如图3位置时,试问:BD与DE,CE具有怎样的等量关系?请写出结果,不必证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣ ![]() x+4交x轴于点A,交y轴于点C,抛物线y=ax2﹣
x+4交x轴于点A,交y轴于点C,抛物线y=ax2﹣ ![]() x+c过点A,交y轴于点B(0,﹣2)
x+c过点A,交y轴于点B(0,﹣2)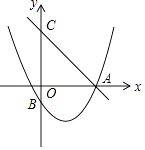
(1)求抛物线的解析式;
(2)点M为抛物线在第四象限部分上的一个动点,求四边形BMAC面积的最大值;
(3)点D为抛物线对称轴上一点,规定:d=|AD﹣BD|,探究d是否存在最大值?若存在,请直接写出d的最大值及此时点D的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com