
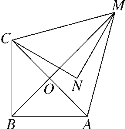
【题目】(题文)如图,在等腰直角三角形MNC中,CN=MN=![]() ,将△MNC绕点C顺时针旋转60°,得到△ABC,连接AM,BM,BM交AC于点O.
,将△MNC绕点C顺时针旋转60°,得到△ABC,连接AM,BM,BM交AC于点O.
(1)∠NCO的度数为________;
(2)求证:△CAM为等边三角形;
(3)连接AN,求线段AN的长.
【答案】(1)15°;(2)证明见解析;(3)![]()
【解析】(1)由旋转可得∠ACM=60°,再根据等腰直角三角形MNC中,∠MCN=45°,运用角的和差关系进行计算即可得到∠NCO的度数;
(2)根据有一个角是60°的等腰三角形是等边三角形进行证明即可;
(3)根据△MNC是等腰直角三角形,△ACM是等边三角形,判定△ACN≌△AMN,再根据Rt△ACD中,AD=![]() CD=
CD=![]() ,等腰Rt△MNC中,DN=
,等腰Rt△MNC中,DN=![]() CM=1,即可得到AN=AD﹣ND=
CM=1,即可得到AN=AD﹣ND=![]() ﹣1.
﹣1.
(1)由旋转可得∠ACM=60°.
又∵等腰直角三角形MNC中,∠MCN=45°,∴∠NCO=60°﹣45°=15°;
故答案为:15°;
(2)∵∠ACM=60°,CM=CA,∴△CAM为等边三角形;
(3)连接AN并延长,交CM于D.
∵△MNC是等腰直角三角形,△ACM是等边三角形,∴NC=NM=![]() ,CM=2,AC=AM=2.在△ACN和△AMN中,∵
,CM=2,AC=AM=2.在△ACN和△AMN中,∵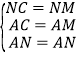 ,∴△ACN≌△AMN(SSS),∴∠CAN=∠MAN,∴AD⊥CM,CD=
,∴△ACN≌△AMN(SSS),∴∠CAN=∠MAN,∴AD⊥CM,CD=![]() CM=1,∴Rt△ACD中,AD=
CM=1,∴Rt△ACD中,AD=![]() CD=
CD=![]() ,等腰Rt△MNC中,DN=
,等腰Rt△MNC中,DN=![]() CM=1,∴AN=AD﹣ND=
CM=1,∴AN=AD﹣ND=![]() ﹣1.
﹣1.


科目:初中数学 来源: 题型:
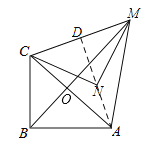
【题目】P是等边△ABC内部一点,∠APB、∠BPC、∠CPA的大小之比是5:6:7,将△ABP逆时针旋转,使得AB与AC重合,则以PA、PB、PC的长为边的三角形的三个角∠PCQ:∠QPC:∠PQC= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=2,BC边上有10个不同的点P1,P2,……,P10, 记![]() (i = 1,2,……,10),那么 M1+M2+……+M10的值为( )
(i = 1,2,……,10),那么 M1+M2+……+M10的值为( )
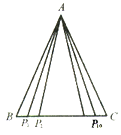
A. 4 B. 14 C. 40 D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量出大楼AB的高度,从距离楼底B处50米的点C(点C与楼底B在同一水平面上)出发,沿倾斜角为30°的斜坡CD前进20米到达点D,在点D处测得楼顶A的仰角为64°,求大楼AB的高度(结果精确到1米)(参考数据:sin64°≈0.9,cos64°≈0.4,tan64°≈2.1, ![]() ≈1.7)
≈1.7)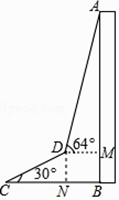
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.
请解决下列问题:
(1)已知点M,N是线段AB的勾股分割点,且BN>MN>AM.若AM=2,MN=3,求BN的长;
(2)如图2,若点F、M、N、G分别是AB、AD、AE、AC边上的中点,点D,E是线段BC的勾股分割点,且EC>DE>BD,求证:点M,N是线段FG的勾股分割点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级(1)班全体学生上周末进行体育测试的成绩(满分70分)统计如表:
成绩(分) | 45 | 50 | 55 | 60 | 65 | 68 | 70 |
人数(人) | 2 | 6 | 10 | 7 | 6 | 5 | 4 |
根据表中的信息判断,下列结论中错误的是( )
A. 该班一共有40名同学
B. 该班学生这次测试成绩的众数是55分
C. 该班学生这次测试成绩的中位数是60分
D. 该班学生这次测试成绩的平均数是59分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲进行了10次射击训练,平均成绩为9环,且前9次的成绩(单位:环)依次为:8,10,9,10,7,9,10,8,10.
(1)求甲第10次的射击成绩;
(2)求甲这10次射击成绩的方差;
(3)乙在相同情况下也进行了10次射击训练,平均成绩为9环,方差为1.6环2,请问甲和乙哪个的射击成绩更稳定?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)分别求出代数式a2﹣2ab+b2和(a﹣b)2的值.
①其中a=![]() ,b=3;②a=5,b=3;③a=﹣1,b=2.
,b=3;②a=5,b=3;③a=﹣1,b=2.
(2)观察(1)中的①②③你发现这两个多项式有什么关系,直接写出.
(3)利用你发现的规律,求出1.4372﹣2×1.437×0.437+0.4372的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
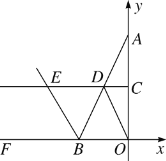
【题目】如图,在平面直角坐标系中,已知点A(0,6),B(b,0),且b<0,C,D分别是OA,AB的中点,△AOB的外角∠DBF的平分线BE与CD的延长线交于点E.
(1)求证:∠DAO=∠DOA;
(2)①若b=-8,求CE的长;
②若CE=![]() +1,则b=________;
+1,则b=________;
(3)是否存在这样的b值,使得四边形OBED为平行四边形?若存在,请求出此时四边形OBED对角线的交点坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com