
【题目】(1)分别求出代数式a2﹣2ab+b2和(a﹣b)2的值.
①其中a=![]() ,b=3;②a=5,b=3;③a=﹣1,b=2.
,b=3;②a=5,b=3;③a=﹣1,b=2.
(2)观察(1)中的①②③你发现这两个多项式有什么关系,直接写出.
(3)利用你发现的规律,求出1.4372﹣2×1.437×0.437+0.4372的值.
【答案】(1)①![]() ;
;![]() ;②4;4;③9;9;(2)a2﹣2ab+b2=(a﹣b)2;(3)1.
;②4;4;③9;9;(2)a2﹣2ab+b2=(a﹣b)2;(3)1.
【解析】
(1)把a与b的值分别代入两式计算即可得到结果;
(2)根据(1)的结果判断即可;
(3)利用得出的规律将原式变形,计算即可得到结果.
解:(1)①当a=![]() ,b=3时,a2﹣2ab+b2=(
,b=3时,a2﹣2ab+b2=(![]() )2﹣2×
)2﹣2×![]() +32=
+32=![]() ;(a﹣b)2=(
;(a﹣b)2=(![]() ﹣3)2=
﹣3)2=![]() ;
;
②当a=5,b=3时,a2﹣2ab+b2=52﹣2×5×3+32=4;(a﹣b)2=(5﹣3)2=4;
③当a=﹣1,b=2时,a2﹣2ab+b2=(﹣1)2﹣2×(﹣1)×2+22=9;(a﹣b)2=(﹣1﹣2)2=9;
(2)a2﹣2ab+b2=(a﹣b)2;
(3)1.4372﹣2×1.437×0.437+0.4372=(1.437﹣0.437)2=1.


科目:初中数学 来源: 题型:
【题目】一慢车和一快车沿相同路线从A地到B地,所行的路程与时间的函数图象如图所示.请你根据图象,回答下列问题: 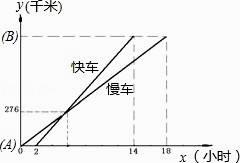
(1)慢车比快车早出发小时,快车追上慢车时行驶了千米,快车比慢车早小时到达B地;
(2)在下列3个问题中任选一题求解(多做不加分): ①快车追上慢车需几个小时?
②求慢车、快车的速度;
③求A、B两地之间的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)如图,在等腰直角三角形MNC中,CN=MN=![]() ,将△MNC绕点C顺时针旋转60°,得到△ABC,连接AM,BM,BM交AC于点O.
,将△MNC绕点C顺时针旋转60°,得到△ABC,连接AM,BM,BM交AC于点O.
(1)∠NCO的度数为________;
(2)求证:△CAM为等边三角形;
(3)连接AN,求线段AN的长.
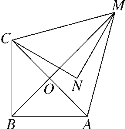
查看答案和解析>>
科目:初中数学 来源: 题型:
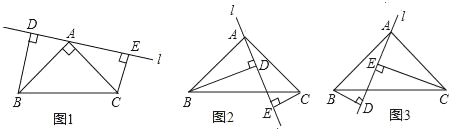
【题目】在△ABC中,∠BAC=90°,AB=AC,l是过A的一条直线,BD⊥AE于D,CE⊥AE于E.求证:
(1)当直线l绕点A旋转到如图1位置时,试说明:DE=BD+CE.
(2)若直线l绕点A旋转到如图2位置时,试说明:DE=BD﹣CE.
(3)若直线l绕点A旋转到如图3位置时,试问:BD与DE,CE具有怎样的等量关系?请写出结果,不必证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=60°,分别引射线OC、OD、OE,使OD平分∠BOC,OE平分∠AOD.
(1)若∠BOC=20°,请依题意补全图形,并求∠BOE的度数;
(2)若∠BOC=α(其中α是小于60°的锐角),请直接写出∠BOE的度数(用含α的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A坐标为(0,3),点B在x轴上 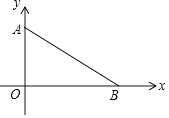
(1)在坐标系中求作一点M,使得点M到点A,点B和原点O这三点的距离相等,在图中保留作图痕迹,不写作法;
(2)若函数y= ![]() 的图象经过点M,且sin∠OAB=
的图象经过点M,且sin∠OAB= ![]() ,求k的值.
,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣ ![]() x+4交x轴于点A,交y轴于点C,抛物线y=ax2﹣
x+4交x轴于点A,交y轴于点C,抛物线y=ax2﹣ ![]() x+c过点A,交y轴于点B(0,﹣2)
x+c过点A,交y轴于点B(0,﹣2)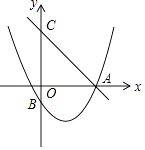
(1)求抛物线的解析式;
(2)点M为抛物线在第四象限部分上的一个动点,求四边形BMAC面积的最大值;
(3)点D为抛物线对称轴上一点,规定:d=|AD﹣BD|,探究d是否存在最大值?若存在,请直接写出d的最大值及此时点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上三点A,O,B对应的数分别为﹣5,0,1,点M为数轴上任意一点,其对应的数为x.
请回答问题:
![]()
(1)A、B两点间的距离是_____,若点M到点A、点B的距离相等,那么x的值是_____;
(2)若点A先沿着数轴向右移动6个单位长度,再向左移动4个单位长度后所对应的数字是 ____ ;
(3)当x为何值时,点M到点A、点B的距离之和是8;
(4)如果点M以每秒3个单位长度的速度从点O向左运动时,点A和点B分别以每秒1个单位长度和每秒4个单位长度的速度也向左运动,且三点同时出发,那么几秒种后点M运动到点A、点B之间,且点M到点A、点B的距离相等?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com