练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】一慢车和一快车沿相同路线从A地到B地，所行的路程与时间的函数图象如图所示．请你根据图象，回答下列问题：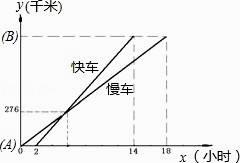
    （1）慢车比快车早出发小时，快车追上慢车时行驶了千米，快车比慢车早小时到达B地；
    （2）在下列3个问题中任选一题求解（多做不加分）： ①快车追上慢车需几个小时？
    ②求慢车、快车的速度；
    ③求A、B两地之间的路程．

    【答案】
    （1）2；276；4
    （2）解：设快车追上慢车时，慢车行驶了x小时，则慢车的速度可以表示为 千米/小时，快车的速度为 千米/小时，根据两车行驶的路程相等，可以列出方程

    解得x=6（小时）．

    所以，

    ①快车追上慢车需6﹣2=4（小时）；

    ②慢车的速度为 千米/小时，快车的速度为 千米/小时；

    ③A、B两地间的路程为46×18=828千米．


    【解析】解：（1）慢车比快车早出发2小时，快车追上慢车时行驶了276千米，快车比慢车早4小时到达B地；

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ACB＝90°，过点C的直线MN∥AB，D为AB边上一点，过点D作DE⊥BC，交直线MN于E，垂足为F，连接CD，BE.

    （1）求证：CE＝AD；

    （2）当D为AB中点时，四边形BECD是什么特殊四边形？说明你的理由；

    （3）若D为AB中点，则当∠A的大小满足什么条件时，四边形BECD是正方形？请说明你的理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】P是等边△ABC内部一点，∠APB、∠BPC、∠CPA的大小之比是5：6：7，将△ABP逆时针旋转，使得AB与AC重合，则以PA、PB、PC的长为边的三角形的三个角∠PCQ：∠QPC：∠PQC= ．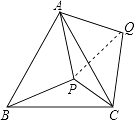

    查看答案和解析>>

    科目：初中数学 来源： 题型：

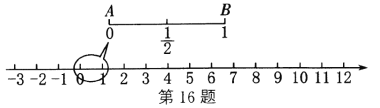
    【题目】陈老师从拉面的制作中受到启发，设计了一个数学问题:如图，在数轴上截取从原点到1的对应点的线段，对折后(点与重合)再均匀地拉成1个单位长度的线段，这一过程称为一次操作(如在第一次操作后，原线段上的和均变成，变成1等).那么在线段上(除、)的点中，在第次操作后，恰好被拉到与1重合的点所对应的数为________________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】复习“全等三角形”的知识时，老师布置了一道作业题：

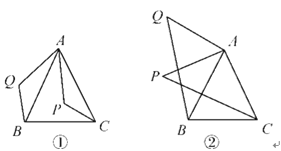
    “如图①，已知，在△ABC中，AB＝AC，P是△ABC内任意一点，将AP绕点A顺时针旋转至AQ，使∠QAP＝∠BAC，连接BQ，CP，则BQ＝CP.”

    小亮是个爱动脑筋的同学，他通过对图①的分析，证明了△ABQ≌△ACP，从而证得BQ＝CP之后，他将点P移到等腰三角形ABC外，原题中其他条件不变，发现“BQ＝CP”仍然成立，请你就图②给出证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线l1：y=x2﹣4的图象与x轴交于A，C两点，抛物线l2与l1关于x轴对称．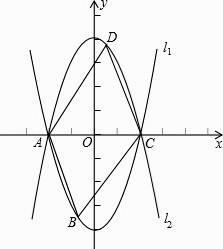

    （1）直接写出l2所对应的函数表达式；
    （2）若点B是抛物线l2上的动点（B与A，C不重合），以AC为对角线，A，B，C三点为顶点的平行四边形的第四个顶点为D，求证：D点在l2上．
    （3）当点B位于l1在x轴下方的图象上，平行四边形ABCD的面积是否存在最大值和最小值？若存在，判断它是何种特殊平行四边形，并求出它面积的最值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，AB＝AC＝2，BC边上有10个不同的点P1，P2，……，P10， 记（i ＝ 1，2，……，10），那么 M1+M2+……+M10的值为（ ）

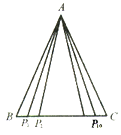
    A. 4 B. 14 C. 40 D. 不能确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了测量出大楼AB的高度，从距离楼底B处50米的点C（点C与楼底B在同一水平面上）出发，沿倾斜角为30°的斜坡CD前进20米到达点D，在点D处测得楼顶A的仰角为64°，求大楼AB的高度（结果精确到1米）（参考数据：sin64°≈0.9，cos64°≈0.4，tan64°≈2.1， ≈1.7）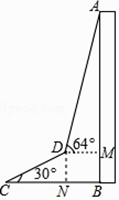

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）分别求出代数式a2﹣2ab+b2和（a﹣b）2的值．

    ①其中a=，b=3；②a=5，b=3；③a=﹣1，b=2．

    （2）观察（1）中的①②③你发现这两个多项式有什么关系，直接写出．

    （3）利用你发现的规律，求出1.4372﹣2×1.437×0.437+0.4372的值．

    查看答案和解析>>

    同步练习册答案