
【题目】复习“全等三角形”的知识时,老师布置了一道作业题:
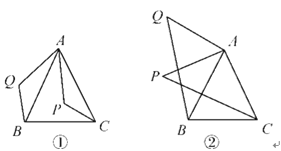
“如图①,已知,在△ABC中,AB=AC,P是△ABC内任意一点,将AP绕点A顺时针旋转至AQ,使∠QAP=∠BAC,连接BQ,CP,则BQ=CP.”
小亮是个爱动脑筋的同学,他通过对图①的分析,证明了△ABQ≌△ACP,从而证得BQ=CP之后,他将点P移到等腰三角形ABC外,原题中其他条件不变,发现“BQ=CP”仍然成立,请你就图②给出证明.
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2的图象如图所示,则关于x的一元二次方程x2+x+a﹣1=0的根的存在情况是( ) 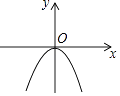
A.没有实数根
B.有两个相等的实数根
C.有两个不相等的实数根
D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某专卖店有 A,B 两种商品.已知在打折前,买 20 件 A 商品和 10 件B 商品用了 400 元;买 30 件 A 商品和 20 件 B 商品用了 640 元.A,B 两种商品打相同折以后,某人买 100 件 A 商品和 200 件 B 商品一共比不打折少花 640 元,计算打了多少折?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一慢车和一快车沿相同路线从A地到B地,所行的路程与时间的函数图象如图所示.请你根据图象,回答下列问题: 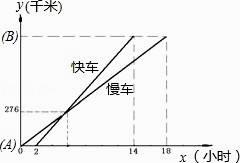
(1)慢车比快车早出发小时,快车追上慢车时行驶了千米,快车比慢车早小时到达B地;
(2)在下列3个问题中任选一题求解(多做不加分): ①快车追上慢车需几个小时?
②求慢车、快车的速度;
③求A、B两地之间的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:Rt△ABC中,∠ACB=90°,CA=3,CB=4,设P,Q分别为AB边,CB边上的动点,它们同时分别从A,C出发,以每秒1个单位长度的速度向终点B运动,设P,Q运动的时间为t秒.
(1)求△CPQ的面积S与运动时间t之间的函数关系式,并求出S的最大值.
(2)t为何值时,△CPQ为直角三角形.
(3)①探索:△CPQ是否可能为正三角形,说明理由.
②P,Q两点同时出发,若点P的运动速度不变,试改变点Q的运动速度,使△CPQ为正三角形,求出点Q的运动速度和此时的t值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
(1)【阅读发现】如图①,在△ABC中,∠ACB=45°,AD⊥BC于点D,E为AD上一点,且DE=BD,可知AB=CE.
(2)【类比探究】如图②,在正方形ABCD中,对角线AC与BD交于点O,E是OC上任意一点,AG⊥BE于点G,交BD于点F.判断AF与BE的数量关系,并加以证明.
(3)【推广应用】在图②中,若AB=4,BF= ![]() ,则△AGE的面积为 .
,则△AGE的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
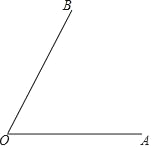
【题目】如图,∠AOB=60°,分别引射线OC、OD、OE,使OD平分∠BOC,OE平分∠AOD.
(1)若∠BOC=20°,请依题意补全图形,并求∠BOE的度数;
(2)若∠BOC=α(其中α是小于60°的锐角),请直接写出∠BOE的度数(用含α的代数式表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com