
【题目】已知二次函数y=ax2的图象如图所示,则关于x的一元二次方程x2+x+a﹣1=0的根的存在情况是( ) 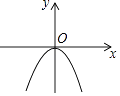
A.没有实数根
B.有两个相等的实数根
C.有两个不相等的实数根
D.无法确定
【答案】C
【解析】解:根据图象得a<0, ∵△=12﹣4(a﹣1)=5﹣4a,
而a<0,
∴△>0,
∴关于x的一元二次方程x2+x+a﹣1=0的有两个不相等的实数根.
故选C.
【考点精析】本题主要考查了二次函数的图象和抛物线与坐标轴的交点的相关知识点,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC在直角坐标系中,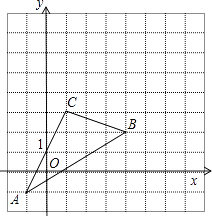
(1)请写出△ABC各点的坐标;
(2)求出S△ABC;
(3)若把△ABC向上平移2个单位,再向右平移2个单位得△A′B′C′,在图中画出△ABC变化位置,并写出A′、B′、C′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆出租车从A地出发,在一条东西走向的街道上往返,每次行驶的情况(记向东为正)记录如下(x>5且x<14,单位:m):
行驶次数 | 第一次 | 第二次 | 第三次 | 第四次 |
行驶情况 | x | ﹣ | x﹣3 | 2(5﹣x) |
行驶方向(填“东”或“西”) |
|
|
|
|
(1)请将表格补充完整;
(2)求经过连续4次行驶后,这辆出租车所在的位置;
(3)若出租车行驶的总路程为41m,求第一次行驶的路程x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一张长方形纸条上画一条数轴.

(1)若折叠纸条,数轴上表示﹣3的点与表示5的点重合,则折痕与数轴的交点表示的数为 ;
(2)若将此纸条沿图中虚线处剪开,将中间的一段纸条对折,使其左右两端重合,这样连续对折2次后,再将其展开,则最左端的折痕和最右端的折痕与数轴的交点表示的数分别是 ;
(3)如果该数轴上的两个点表示的数为a和b,经过对折,两点恰好重合,则折痕与数轴的交点表示的数为 ;(用含a,b的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了更好的开展“学校特色体育教育”,从全校八年级各班随机抽取了60学生,进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据,得到的关于每个个体的测试成绩的部分统计表、图: 某校60名学生体育测试成绩成绩统计表
成绩 | 划记 | 频数 | 频率 |
优秀 | 正正正 | a | 0.3 |
良好 | 正正正正正正 | 30 | b |
合格 | 正 | 9 | 0.15 |
不合格 |
| c | d |
合计 |
(说明:40﹣55分为不合格,55﹣70分为合格,70﹣85分为良好,85﹣100分为优秀)
请根据以上信息,解答下列问题:
(1)表中的a=;b=;c=;d= .
(2)请根据频数分布表,画出相应的频数分布直方图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2016次相遇地点的坐标是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农户承包种植某水果,今年投资30 000元,收获水果20 000千克.此水果在市场上的售价为每千克![]() 元,卖给到果园收购的商贩每千克
元,卖给到果园收购的商贩每千克![]() 元(
元(![]() .若农户将水果拉到市场上出售,则平均每天可售1000千克,需雇佣2人,每人每天付工资150元,运输及其他税费平均每天200元.
.若农户将水果拉到市场上出售,则平均每天可售1000千克,需雇佣2人,每人每天付工资150元,运输及其他税费平均每天200元.
(1)分别用含![]() 的代数式表示两种出售方式的纯收入.
的代数式表示两种出售方式的纯收入.
(2)若![]() ,且两种出售方式在相同的时间内售完全部水果.请通过计算说明哪种出售方式较好.
,且两种出售方式在相同的时间内售完全部水果.请通过计算说明哪种出售方式较好.
(3)该农户总结今年的种植及销售的经验,加强果园管理,力争明年纯收入达到100000元,则与(2)中今年较好的出售方式的纯收入相比,明年的纯收入的增长率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】复习“全等三角形”的知识时,老师布置了一道作业题:
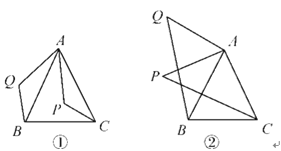
“如图①,已知,在△ABC中,AB=AC,P是△ABC内任意一点,将AP绕点A顺时针旋转至AQ,使∠QAP=∠BAC,连接BQ,CP,则BQ=CP.”
小亮是个爱动脑筋的同学,他通过对图①的分析,证明了△ABQ≌△ACP,从而证得BQ=CP之后,他将点P移到等腰三角形ABC外,原题中其他条件不变,发现“BQ=CP”仍然成立,请你就图②给出证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com