
【题目】在△ABC中,∠BAC=90°,AB=AC,l是过A的一条直线,BD⊥AE于D,CE⊥AE于E.求证:
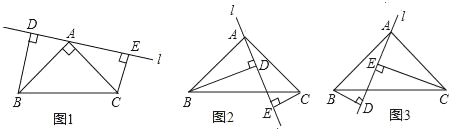
(1)当直线l绕点A旋转到如图1位置时,试说明:DE=BD+CE.
(2)若直线l绕点A旋转到如图2位置时,试说明:DE=BD﹣CE.
(3)若直线l绕点A旋转到如图3位置时,试问:BD与DE,CE具有怎样的等量关系?请写出结果,不必证明.
【答案】(1)证明见解析(2)证明见解析(3)DE=CE﹣BD
【解析】
(1) 利用条件证明△ABD≌△CAE, 再结合线段的和差可得出结论;
(2) 同 (1) 可证明△ABD≌△CAE, 再结合线段的和差可得出结论;
(3) 同理可证明△ABD≌△CAE, 再结合线段的和差可得出结论.
(1)证明:如图1,∵BD⊥l,CE⊥l,
∴∠BDA=∠CEA=90°,
∴∠ABD+∠DAB=90°.
∵∠BAC=90°,
∴∠DAB+∠CAE=90°,
∴∠ABD=∠CAE.
在△ABD和△CAE中,
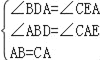 ,
,
∴△ABD≌△CAE(AAS),
∴AD=CE,BD=AE.
∵DE=AD+AE,
∴DE=CE+BD;
(2)如图2,∵BD⊥l,CE⊥l,
∴∠BDA=∠CEA=90°,
∴∠ABD+∠DAB=90°.
∵∠BAC=90°,
∴∠DAB+∠CAE=90°,∴∠ABD=∠CAE.
在△ABD和△CAE中,
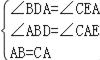 ,
,
∴△ABD≌△CAE(AAS),
∴AD=CE,BD=AE
∵DE=AE﹣AD,
∴DE=BD﹣CE.
(3)DE=CE﹣BD
如图3,∵BD⊥l,CE⊥l,
∴∠BDA=∠CEA=90°,
∴∠ABD+∠DAB=90°.
∵∠BAC=90°,
∴∠DAB+∠CAE=90°,
∴∠ABD=∠CAE.
在△ABD和△CAE中,
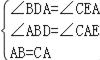 ,
,
∴△ABD≌△CAE(AAS),
∴AD=CE,BD=AE
∵DE=AD﹣AE,
∴DE=CE﹣BD.


 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:
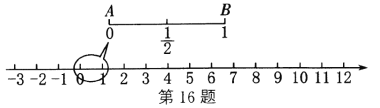
【题目】陈老师从拉面的制作中受到启发,设计了一个数学问题:如图,在数轴上截取从原点到1的对应点的线段![]() ,对折后(点
,对折后(点![]() 与
与![]() 重合)再均匀地拉成1个单位长度的线段,这一过程称为一次操作(如在第一次操作后,原线段
重合)再均匀地拉成1个单位长度的线段,这一过程称为一次操作(如在第一次操作后,原线段![]() 上的
上的![]() 和
和![]() 均变成
均变成![]() ,
,![]() 变成1等).那么在线段
变成1等).那么在线段![]() 上(除
上(除![]() 、
、![]() )的点中,在第
)的点中,在第![]() 次操作后,恰好被拉到与1重合的点所对应的数为________________.
次操作后,恰好被拉到与1重合的点所对应的数为________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量出大楼AB的高度,从距离楼底B处50米的点C(点C与楼底B在同一水平面上)出发,沿倾斜角为30°的斜坡CD前进20米到达点D,在点D处测得楼顶A的仰角为64°,求大楼AB的高度(结果精确到1米)(参考数据:sin64°≈0.9,cos64°≈0.4,tan64°≈2.1, ![]() ≈1.7)
≈1.7)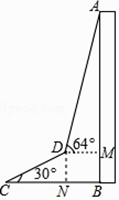
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级(1)班全体学生上周末进行体育测试的成绩(满分70分)统计如表:
成绩(分) | 45 | 50 | 55 | 60 | 65 | 68 | 70 |
人数(人) | 2 | 6 | 10 | 7 | 6 | 5 | 4 |
根据表中的信息判断,下列结论中错误的是( )
A. 该班一共有40名同学
B. 该班学生这次测试成绩的众数是55分
C. 该班学生这次测试成绩的中位数是60分
D. 该班学生这次测试成绩的平均数是59分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲进行了10次射击训练,平均成绩为9环,且前9次的成绩(单位:环)依次为:8,10,9,10,7,9,10,8,10.
(1)求甲第10次的射击成绩;
(2)求甲这10次射击成绩的方差;
(3)乙在相同情况下也进行了10次射击训练,平均成绩为9环,方差为1.6环2,请问甲和乙哪个的射击成绩更稳定?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列一元一次方程解应用题:
社会是一个重要的学校和课堂,生活是一种重要的课程和教材,实践是一种重要的学习方式和途径.参加社会生活和社会实践,不仅可以学到很多在课堂上学不到的东西,也可以把课堂上学到的理论知识同社会实践联系起来,加深对课堂学习内容的理解,我区某校七年级学生在农场进行社会实践活动时,采摘了黄瓜和茄子共80千克,了解到这些蔬菜的种植成本共180元,还了解到如下信息:

(1)求采摘的黄瓜和茄子各多少千克?
(2)这些采摘的黄瓜和茄子可赚多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)分别求出代数式a2﹣2ab+b2和(a﹣b)2的值.
①其中a=![]() ,b=3;②a=5,b=3;③a=﹣1,b=2.
,b=3;②a=5,b=3;③a=﹣1,b=2.
(2)观察(1)中的①②③你发现这两个多项式有什么关系,直接写出.
(3)利用你发现的规律,求出1.4372﹣2×1.437×0.437+0.4372的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列计算:
(1)78-23÷70=70÷70=1;
(2)12-7×(-4)+8÷(-2)=12+28-4=36;
(3)12÷(2×3)=12÷2×3=6×3=18;
(4)32×3.14+3×(-9.42)=3×9.42+3×(-9.42)=0.
其中错误的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
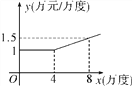
【题目】某工厂在生产过程中每消耗1万度电可以产生产值5.5万元,电力公司规定,该工厂每月用电量不得超过16万度;月用电量不超过4万度时,单价都是1万元/万度;超过4万度时,超过部分电量单价将按用电量进行调整.电价y与月用电量x的函数关系可以用下图来表示(效益=产值-用电量×电价).
(1)求y与月用电量x之间的函数关系式,并写出自变量的取值范围;
(2)设工厂的月效益为z(万元),写出z与用电量x之间的函数关系式;
(3)求工厂最大月效益.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com