
【题目】如图所示,△ABC中,∠A=90°,D是AC上一点,且∠ADB=2∠C,P是BC上任一点,PE⊥BD于点E,PF⊥AC于点F,下列结论:
①△DBC是等腰三角形;②∠C=30°;③PE+PF=AB;④PE2+AF2=BP2.
其中结论正确的个数是( )
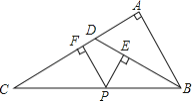
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ADB=∠C+∠DBC,然后求出∠C=∠DBC,再根据等角对等边可得DC=DB,从而判断①正确;没有条件说明∠C的度数,判断出②错误;连接PD,利用△BCD的面积列式求解即可得到PE+PF=AB,判断出③正确;过点B作BG∥AC交FP的延长线于G,根据两直线平行,内错角相等可得∠C=∠PBG,∠G=∠CFP=90°,然后求出四边形ABGF是矩形,根据矩形的对边相等可得AF=BG,根据然后利用“角角边”证明△BPE和△BPG全等,根据全等三角形对应边相等可得BG=BE,再利用勾股定理列式求解即可判断④正确.
在 △BCD 中, ∠ADB=∠C+∠DBC ,
∵∠ADB=2∠C ,
∴∠C=∠DBC ,
∴DC=DB ,
∴△DBC 是等腰三角形,故①正确;
无法说明 ∠C=30° ,故②错误;
连接 PD ,则 S△BCD=![]() BDPE+
BDPE+![]() DCPF=
DCPF=![]() DCAB,
DCAB,
∴PE+PF=AB ,故③正确;
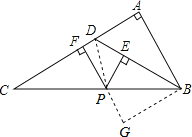
过点 B 作 BG ∥ AC 交 FP 的延长线于 G ,
则 ∠C=∠PBG , ∠G=∠CFP=90° ,
∴∠PBG=∠DBC ,四边形 ABGF 是矩形,
∴AF=BG ,
在 △BPE 和 △BPG 中,
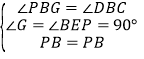 ,
,
∴△BPE ≌ △BPG(AAS) ,
∴BG=BE ,
∴AF=BE ,
在 Rt△PBE 中, PE +BE =BP ,
即 PE +AF =BP ,故④正确。
综上所述,正确的结论有①③④。
故选C.


科目:初中数学 来源: 题型:
【题目】有一个运算装置,当输入值为x时,其输出值为y,且y是x的二次函数,已知输入值为﹣2,0,1时,相应的输出值分别为5,﹣3,﹣4. 
(1)求此二次函数的解析式;
(2)在所给的坐标系中画出这个二次函数的图象,并根据图象写出当输出值y为正数时输入值x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方体的长BE=15cm,宽AB=10cm,高AD=20cm,点M在CH上,且CM=5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点M,需要爬行的最短距离是多少?
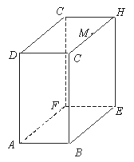
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农户承包种植某水果,今年投资30 000元,收获水果20 000千克.此水果在市场上的售价为每千克![]() 元,卖给到果园收购的商贩每千克
元,卖给到果园收购的商贩每千克![]() 元(
元(![]() .若农户将水果拉到市场上出售,则平均每天可售1000千克,需雇佣2人,每人每天付工资150元,运输及其他税费平均每天200元.
.若农户将水果拉到市场上出售,则平均每天可售1000千克,需雇佣2人,每人每天付工资150元,运输及其他税费平均每天200元.
(1)分别用含![]() 的代数式表示两种出售方式的纯收入.
的代数式表示两种出售方式的纯收入.
(2)若![]() ,且两种出售方式在相同的时间内售完全部水果.请通过计算说明哪种出售方式较好.
,且两种出售方式在相同的时间内售完全部水果.请通过计算说明哪种出售方式较好.
(3)该农户总结今年的种植及销售的经验,加强果园管理,力争明年纯收入达到100000元,则与(2)中今年较好的出售方式的纯收入相比,明年的纯收入的增长率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,BD为AC边上的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若AG=13,BG=5,则CF的长为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】P是等边△ABC内部一点,∠APB、∠BPC、∠CPA的大小之比是5:6:7,将△ABP逆时针旋转,使得AB与AC重合,则以PA、PB、PC的长为边的三角形的三个角∠PCQ:∠QPC:∠PQC= . 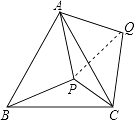
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】陈老师从拉面的制作中受到启发,设计了一个数学问题:如图,在数轴上截取从原点到1的对应点的线段![]() ,对折后(点
,对折后(点![]() 与
与![]() 重合)再均匀地拉成1个单位长度的线段,这一过程称为一次操作(如在第一次操作后,原线段
重合)再均匀地拉成1个单位长度的线段,这一过程称为一次操作(如在第一次操作后,原线段![]() 上的
上的![]() 和
和![]() 均变成
均变成![]() ,
,![]() 变成1等).那么在线段
变成1等).那么在线段![]() 上(除
上(除![]() 、
、![]() )的点中,在第
)的点中,在第![]() 次操作后,恰好被拉到与1重合的点所对应的数为________________.
次操作后,恰好被拉到与1重合的点所对应的数为________________.
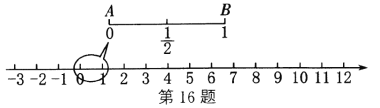
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量出大楼AB的高度,从距离楼底B处50米的点C(点C与楼底B在同一水平面上)出发,沿倾斜角为30°的斜坡CD前进20米到达点D,在点D处测得楼顶A的仰角为64°,求大楼AB的高度(结果精确到1米)(参考数据:sin64°≈0.9,cos64°≈0.4,tan64°≈2.1, ![]() ≈1.7)
≈1.7)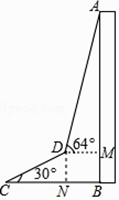
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com