
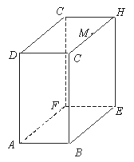
【题目】如图,长方体的长BE=15cm,宽AB=10cm,高AD=20cm,点M在CH上,且CM=5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点M,需要爬行的最短距离是多少?
【答案】25cm
【解析】分析: 将立体图形展开成平面图形,然后根据两点之间线段距离最短,利用根据勾股定理进行求解,根据立体展开成平面图形情况分类讨论进行进行比较.
详解:将长方体沿CH,HE,BE剪开翻折,使面ABCD和面BEHC在同一个平面内,连接AM,如图1,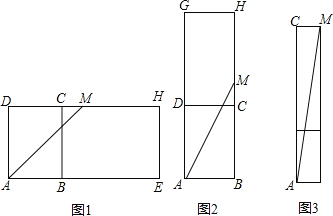
由题意可得:MD=MC+CD=5+10=15cm,AD=20cm,
在Rt△ADM中,根据勾股定理得:AM=25cm,
将长方体沿CH、GD、GH剪开翻折,使面ABCD和面DCHG在同一个平面内,连接AM,
如图2,由题意得:BM=BC+MC=20+5=25(cm),AB=10cm,
在Rt△ABM中,根据勾股定理得:AM=5![]() cm,
cm,
将长方体沿CD、CH、GH剪开翻折,连接AM,如图3,
由题意得:AC=AB+BC=10+20=30(cm),MC=5cm,
在Rt△ACM中,根据勾股定理得:AM=5![]() cm,
cm,
∵25<5![]() <5
<5![]() ,
,
则需要爬行的最短距离是25cm.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】![]() 两地盛产柑桔,
两地盛产柑桔,![]() 地有柑桔200吨,
地有柑桔200吨,![]() 地有柑桔300吨.现将这些柑桔运到C、D两个冷藏仓库,已知
地有柑桔300吨.现将这些柑桔运到C、D两个冷藏仓库,已知![]() 仓库可储存240吨,
仓库可储存240吨,![]() 仓库可储存260吨;从
仓库可储存260吨;从![]() 地运往C、D两处的费用分别为每吨20元和25元,从
地运往C、D两处的费用分别为每吨20元和25元,从![]() 地运往C、D两处的费用分别为每吨15元和18元.设从
地运往C、D两处的费用分别为每吨15元和18元.设从![]() 地运往
地运往![]() 仓库的柑桔重量为x吨,A、B两地运往两仓库的柑桔运输费用分别为yA元和yB元.
仓库的柑桔重量为x吨,A、B两地运往两仓库的柑桔运输费用分别为yA元和yB元.
(1)请填写下表后分别求出yA,yB之间的函数关系式,并写出定义域;
| C | D | 总计 |
A | x吨 | 200吨 | |
B | 300吨 | ||
总计 | 240吨 | 260吨 | 500吨 |
(2)试讨论A,B两地中,哪个运费较少;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一块菱形菜地ABCD中,对角线AC与BD相交于点O,若在菱形菜地内均匀地撒上种子,则种子落在阴影部分的概率是( ) 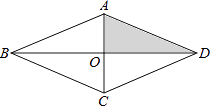
A.1
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠BAD=60°,点M是AB的中点,P是对角线AC上的一个动点,若PM+PB的最小值是9,则AB的长是( ) 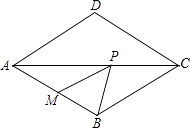
A.6 ![]()
B.3 ![]()
C.9
D.4.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中错误的有( )个
①绝对值相等的两数相等.②若a,b互为相反数,则![]() =﹣1.③如果a大于b,那么a的倒数小于b的倒数.④任意有理数都可以用数轴上的点来表示.⑤x2﹣2x﹣33x3+25是五次四项.⑥两个负数比较大小,绝对值大的反而小.⑦一个数的相反数一定小于或等于这个数.⑧正数的任何次幂都是正数,负数的任何次幂都是负数.
=﹣1.③如果a大于b,那么a的倒数小于b的倒数.④任意有理数都可以用数轴上的点来表示.⑤x2﹣2x﹣33x3+25是五次四项.⑥两个负数比较大小,绝对值大的反而小.⑦一个数的相反数一定小于或等于这个数.⑧正数的任何次幂都是正数,负数的任何次幂都是负数.
A. 4个 B. 5个 C. 6个 D. 7个
查看答案和解析>>
科目:初中数学 来源: 题型:
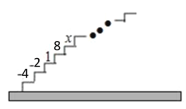
【题目】如图,阶梯图的每个台阶上都标着一个数,从下到上的第1个至第4个台阶上依次标着﹣4,﹣2,1,8,且任意相邻四个台阶上数的和都相等.
尝试:(1)求前4个台阶上数的和是多少?
(2)求第5个台阶上的数x是多少?
应用: 求从下到上39个台阶上数的和.
发现:试用含k(k为正整数)的代数式表示出数“1”所在的台阶数.
查看答案和解析>>
科目:初中数学 来源: 题型:
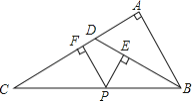
【题目】如图所示,△ABC中,∠A=90°,D是AC上一点,且∠ADB=2∠C,P是BC上任一点,PE⊥BD于点E,PF⊥AC于点F,下列结论:
①△DBC是等腰三角形;②∠C=30°;③PE+PF=AB;④PE2+AF2=BP2.
其中结论正确的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
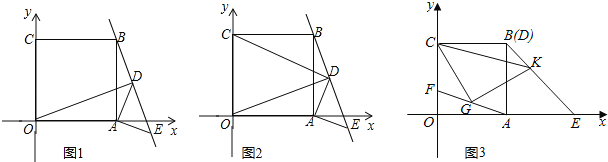
【题目】在平面直角坐标系中,正方形OABC的两边OA、OC分别落在x轴、y轴的正半轴上,等腰Rt△ADE的两个顶点D、E和正方形顶点B三点在一条直线上.
(1)如图1,连接OD,求证:△OAD≌△BAE;
(2)如图2,连接CD,求证:BE﹣![]() DE=
DE=![]() CD;
CD;
(3)如图3,当图1中的Rt△ADE的顶点D与点B重合时,点E正好落在x轴上,F为线段OC上一动点(不与O、C重合),G为线段AF的中点,若CG⊥GK交BE于点K时,请问∠KCG的大小是否变化?若不变,请求其值;若改变,求出变化的范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com