
【题目】如图①,在△ABC中,AB=AC,∠BAC=![]() (
(![]() <45°).先将△ABC以点B为旋转 中心,逆时针旋转90°得到△DBE,再将△ABC以点A为旋转中心,顺时针旋转90°得到△AFG,连接DF,DG,AE,如图②.
<45°).先将△ABC以点B为旋转 中心,逆时针旋转90°得到△DBE,再将△ABC以点A为旋转中心,顺时针旋转90°得到△AFG,连接DF,DG,AE,如图②.
(1)四边形ABDF的形状是 ;
(2)求证:四边形AEDG是平行四边形;
(3)若AB=2,![]() =30°,则四边形AEDG的面积是 .
=30°,则四边形AEDG的面积是 .

【答案】(1)正方形;(2)见解析;(3)![]()
【解析】
(1)由旋转的性质和旋转角度可求得DE∥AF,且DE=AF,可证明四边形AFDE为平行四边形,再由旋转角是90°,即可得出结论;
(2)由旋转的性质和旋转角度判断出△ABE≌△DFG即可得出结论.
(3)过B作BH⊥AC于H,过点E作EM⊥AB于M,作∠BEN=∠ABE交AB于N,利用直角三角形的性质分别求出BH,AH,CH,BE,BC,计算出∠MNE=30°,设ME=x,则NE=2x,BN=x,利用勾股定理Rt△BME中解出x值,即ME的长度,再利用S四边形AEDG=S正方形ABDF-2S△DBE-2S△ABE计算结果即可.
解:(1)四边形ABDF是正方形,
证明:∵△DBE是由△ABC绕点B逆时针旋转90°得到的,△AFG是由△ABC绕点A顺时针旋转90°得到的,
∴∠DBA=∠FAB=90°,DB=AB=AF,AC=DE=AG,
∴∠DBA+∠FAB=180°,
∴DB∥AF,
∵AB=AC,
∴AB=DB=FA=AC=DE=AG,
∵DB∥AF,DB=AF
∴四边形ABDF是平行四边形,
∵∠ABD=90°,
∴四边形ABDF是矩形,
∵AB=DB,
∴平行四边形ABDF是正方形;
(2)∵四边形ABDF是正方形,
∴∠DFA=∠DBA=90°,AB=DF,
∴∠ABD-∠DBE=∠AFD-∠AFG,
∴∠EBA=∠GFD,
在△ABE和△DFG中,
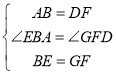 ,
,
∴△ABE≌△DFG(SAS),
∴AE=DG,
又∵DE=AG=AB,
∴四边形AEDG是平行四边形.
(3)过B作BH⊥AC于H,过点E作EM⊥AB于M,作∠BEN=∠ABE交AB于N,
∵AB=2,∠BAC=30°,
∴BH=![]() AB=1,
AB=1,
AH=![]() ,
,
∴CH=AC-AH=AB-AH=2-![]() ,
,
∴BC=![]() =
=![]() ,
,
∴BE=BC=![]() ,
,
∵∠BDE=∠BAC=α=30°,DB=DE,
∴∠DBE=∠DEB=![]() =75°,
=75°,
∴∠ABE=∠ABD-∠DBE=90°-75°=15°,
∴∠BEN=∠ABE=15°,
∴∠MNE=∠NBE+∠BEN=15°+15°=30°,
设ME=x,则NE=2x,BN=x,
MN=![]() ,
,
∴BM=BN+NM=2x+![]() x,
x,
在Rt△BME中,BM2+ME2=BE2,
即![]() ,
,
解得![]() ,
,![]() (舍),
(舍),
∴x=![]() ,
,
∴ME=![]() ,
,
∴S△DBE=S△ABC=![]() AC×BH=
AC×BH=![]() ×2×1=1,
×2×1=1,
S△ABE=![]() AB×ME=
AB×ME=![]() ×2×(
×2×(![]() )=
)=![]() ,
,
∴S四边形AEDG
=S正方形ABDF-2S△DBE-2S△ABE
=![]()
=![]()



 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
【题目】某工厂制作![]() 两种手工艺品,
两种手工艺品,![]() 每天每件获利比
每天每件获利比![]() 多105元,获利30元的
多105元,获利30元的![]() 与获利240元的
与获利240元的![]() 数量相等.
数量相等.
(1)制作一件![]() 和一件
和一件![]() 分别获利多少元?
分别获利多少元?
(2)工厂安排65人制作![]() ,
,![]() 两种手工艺品,每人每天制作2件
两种手工艺品,每人每天制作2件![]() 或1件
或1件![]() .现在在不增加工人的情况下,增加制作
.现在在不增加工人的情况下,增加制作![]() .已知每人每天可制作1件
.已知每人每天可制作1件![]() (每人每天只能制作一种手工艺品),要求每天制作
(每人每天只能制作一种手工艺品),要求每天制作![]() ,
,![]() 两种手工艺品的数量相等.设每天安排
两种手工艺品的数量相等.设每天安排![]() 人制作
人制作![]() ,
,![]() 人制作
人制作![]() ,写出
,写出![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(3)在(1)(2)的条件下,每天制作![]() 不少于5件.当每天制作5件时,每件获利不变.若每增加1件,则当天平均每件获利减少2元.已知
不少于5件.当每天制作5件时,每件获利不变.若每增加1件,则当天平均每件获利减少2元.已知![]() 每件获利30元,求每天制作三种手工艺品可获得的总利润
每件获利30元,求每天制作三种手工艺品可获得的总利润![]() (元)的最大值及相应
(元)的最大值及相应![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国内猪肉价格不断上涨,已知今年10月的猪肉价格比今年年初上涨了80%,李奶奶10月在某超市购买1千克猪肉花了72元钱.
(1)今年年初猪肉的价格为每千克多少元?
(2)某超市将进货价为每千克55元的猪肉按10月价格出售,平均一天能销售出100千克,随着国家对猪肉价格的调控,超市发现猪肉的售价每千克下降1元,其日销售量就增加10千克,超市为了实现销售猪肉每天有1800元的利润,并且尽可能让顾客得到实惠,猪肉的售价应该下降多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校团委决定从4名学生会干部(小明、小华、小丽和小颖)中抽签确定2名同学去进行宣传活动,抽签规则:将4名同学姓名分别写在4张完全相同的卡片正面,把四张卡片背面朝上,洗匀后放在桌面上,既然从中随机抽取一张卡片,记下姓名,再从剩余的3张卡片中随机抽取第二张,记下姓名.试用画树状图或列表的方法表示这次抽签所有可能的结果,并求出小明被抽中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
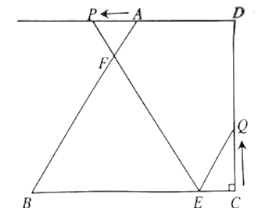
【题目】如图,在四边形![]() 中,
中,![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() 同时,点
同时,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() .过点
.过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连
,连![]() 接,交
接,交![]() 于点
于点![]() .设运动时间为
.设运动时间为![]() .解答下列问题:
.解答下列问题:
(1)当![]() 为何值时,
为何值时,![]() ?
?
(2)设五边形![]() 的面积为
的面积为![]() , 求
, 求![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)连接![]() .是否存在某一时刻
.是否存在某一时刻![]() , 使点
, 使点![]() 在
在![]() 的垂直平分线上,若存在,求出的值;若不存在,说明理由.
的垂直平分线上,若存在,求出的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
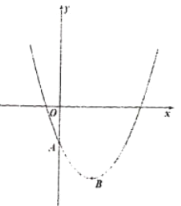
【题目】在平面直角坐标系中,已知如图所示的抛物线顶点![]() 的坐标为
的坐标为![]() ,且过点
,且过点![]() .
.
(1)求该抛物线的解析式;
(2)若点![]() 为抛物线对称轴右侧、
为抛物线对称轴右侧、![]() 轴下方一点,当
轴下方一点,当![]() 时,求直线
时,求直线![]() 的解析式;
的解析式;
(3)平移(1)中的抛物线,记平移后抛物线的顶点为![]() ,顶点
,顶点![]() 在直线
在直线![]() 上滑动,且平移后的抛物线与直线
上滑动,且平移后的抛物线与直线![]() 交于另一点
交于另一点![]() ,若点
,若点![]() 为平移前(1)中抛物线上的点,则当以
为平移前(1)中抛物线上的点,则当以![]() 、
、![]() 、
、![]() 三点为顶点的三角形是等腰直角三角形时,求出所有符合条件的点
三点为顶点的三角形是等腰直角三角形时,求出所有符合条件的点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com