
【题目】如图,![]() 、
、![]() 是等腰
是等腰![]() 两腰上的高,
两腰上的高,![]() 、
、![]() 相交于点
相交于点![]() .
.
(1)求证:![]() ;
;
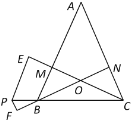
(2)点![]() 在边
在边![]() 的延长线上,过
的延长线上,过![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,作
,作![]() 交
交![]() 的延长线于点
的延长线于点![]() .求证:
.求证:![]() .
.
【答案】(1)证明见解析;(2)证明见解析
【解析】
(1)根据“AAS”证明△BMC≌△CNB,可得∠OBC=∠OCB,再根据经等角对等边可证结论成立;
(2)由![]() =
=![]() -
-![]() ,可得PE-PF=BM,由△BOM∽△BAN,得
,可得PE-PF=BM,由△BOM∽△BAN,得![]() ,再证明AM=AN,代入整理可证结论成立.
,再证明AM=AN,代入整理可证结论成立.
解:(1)∵等腰△ABC中,AB=AC,
∴∠ABC=∠ACB,
∵CM⊥AB,BN⊥AC,
∴∠BMC=∠CNB=90°,
又∵BC=BC,
∴△BMC≌△CNB,
∴∠OBC=∠OCB,
∴OB=OC;
(2)连接OP,
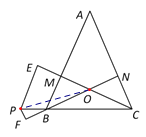
∵PE//AB,PF//AC,
∴∠PEC=∠BMC=90°,∠PFB=∠CNB=90°.
∵![]() =
=![]() -
-![]() ,
,
∴![]() OC·BM=
OC·BM=![]() OC·PE-
OC·PE-![]() OB·PF,
OB·PF,
∵OB=OC,
∴PE-PF=BM.
∵∠BMC=∠ANB=90°,∠BMO=∠NBA,
∴△BOM∽△BAN,
∴![]() ,
,
∴OM·BN=BM·AN=(PE-PF)·AN.
∵△BMC≌△CNB,
∴BM=CN,
∵AB=AC,
∴AM=AN,
∴OM·BN=(PE-PF)·AM,
∴AM·PF+OM·BN=AM·PE.


科目:初中数学 来源: 题型:
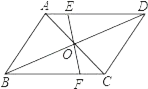
【题目】如图,平行四边形ABCD的对角线AC,BD交于O,EF过点O与AD,BC分别交于E,F,若AB=4,BC=5,OE=1.5,则四边形EFCD的周长_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学就本校学生对新冠肺炎防控有关知识的了解情况进行了一次随机抽样调查,图①、图②是他们根据采集数据绘制的两幅不完整的统计图(A:了解很少,B:了解一般,C:了解较多,D:了解很多).请你根据图中提供的信息解答以下问题:

(1)求本次抽取的学生人数;
(2)先求出![]() 、
、![]() 两类学生人数,然后将图②补充完整;
两类学生人数,然后将图②补充完整;
(3)在扇形统计图中,计算出![]() 部分所对应的扇形圆心角的度数;
部分所对应的扇形圆心角的度数;
(4)若该学校共有1200名学生,请估计![]() 类的学生人数.
类的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
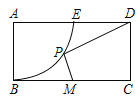
【题目】如图,矩形ABCD中,AB=2,AD=4,M点是BC的中点,A为圆心,AB为半径的圆交AD于点E.点P在弧BE上运动,则PM+![]() DP的最小值为____________.
DP的最小值为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC中,AB=AC,∠BAC=![]() (
(![]() <45°).先将△ABC以点B为旋转 中心,逆时针旋转90°得到△DBE,再将△ABC以点A为旋转中心,顺时针旋转90°得到△AFG,连接DF,DG,AE,如图②.
<45°).先将△ABC以点B为旋转 中心,逆时针旋转90°得到△DBE,再将△ABC以点A为旋转中心,顺时针旋转90°得到△AFG,连接DF,DG,AE,如图②.
(1)四边形ABDF的形状是 ;
(2)求证:四边形AEDG是平行四边形;
(3)若AB=2,![]() =30°,则四边形AEDG的面积是 .
=30°,则四边形AEDG的面积是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
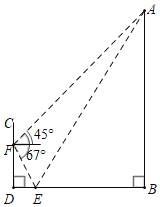
【题目】为了测量竖直旗杆AB的高度,某综合实践小组在地面D处竖直放置标杆CD,并在地面上水平放置一个平面镜E,使得B,E,D在同一水平线上(如图所示).该小组在标杆的F处通过平面镜E恰好观测到旗杆顶A(此时∠AEB=∠FED),在F处测得旗杆顶A的仰角为45°,平面镜E的俯角为67°,测得FD=2.4米.求旗杆AB的高度约为多少米?(结果保留整数,参考数据:sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,抛物线![]() 与
与![]() 轴交于点A和点C(2,0),与
轴交于点A和点C(2,0),与![]() 轴交于点D,将△DOC绕点O逆时针旋转90°后,点D恰好与点A重合,点C与点B重合.
轴交于点D,将△DOC绕点O逆时针旋转90°后,点D恰好与点A重合,点C与点B重合.
(1)直接写出点A和点B的坐标;
(2)求![]() 和
和![]() 的值;
的值;
(3)已知点E是该抛物线的顶点,求证:AB⊥EB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线![]() 与双线
与双线![]() 交于
交于![]() 、
、![]() 两点,
两点,![]() 为第三象限内一点.
为第三象限内一点.
(1)如图1,若点![]() 的坐标为
的坐标为![]() .
.
①![]() ______,点
______,点![]() 的坐标为______.
的坐标为______.
②不等式![]() 的解集为______.
的解集为______.
③当![]() ,且
,且![]() 时,求点
时,求点![]() 的坐标.
的坐标.
(2)如图2,当![]() 为等边三角形时,点
为等边三角形时,点![]() 的坐标为
的坐标为![]() ,试求
,试求![]() 、
、![]() 之间的关系式.
之间的关系式.
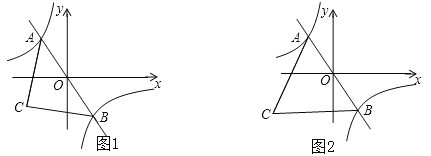
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com