
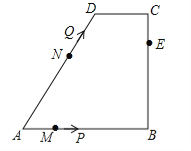
����Ŀ����ͼ�����ı���ABCD�У�AB��CD����B=90�㣬AB=AD=5��BC=4��M��N��E�ֱ���AB��AD��CB�ϵĵ㣬AM=CE=1��AN=3����P�ӵ�M��������ÿ��1����λ���ȵ��ٶ�������MB��BE���E�˶���ͬʱ��Q�ӵ�N����������ͬ���ٶ�������ND��DC��CE���E�˶���������һ���㵽�����һ����Ҳֹͣ�˶�������APQ�����ΪS���˶�ʱ��Ϊt�룬��S��t������ϵ�Ĵ���ͼ��Ϊ�� ��
A��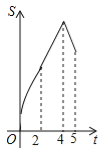 B��
B��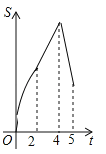 C��
C��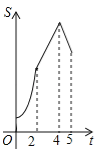 D��
D��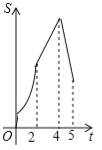
���𰸡�D��
����������AD=5��AN=3����DN=2����ͼ1������D��DF��AB����DF=BC=4����RT��ADF�У�AD=5��DF=4�����ݹ��ɶ����ã�AF=![]() =3����BF=CD=2������Q����Dʱ����2s������PҲ�˶�2s����AP=3����QP��AB����ֻ�����������
=3����BF=CD=2������Q����Dʱ����2s������PҲ�˶�2s����AP=3����QP��AB����ֻ�����������
�ٵ�0��t��2ʱ����ͼ1����Q��QG��AB������D��DF��AB��QG��DF����![]() ��������ã�NQ=t��MP=t����AM=1��AN=3����AQ=t+3����
��������ã�NQ=t��MP=t����AM=1��AN=3����AQ=t+3����![]() ����QG=
����QG=![]() ��t+3������AP=t+1����S=S��APQ=
��t+3������AP=t+1����S=S��APQ=![]() AP��QG=
AP��QG=![]() ����t+1����
����t+1����![]() ��t+3��=
��t+3��=![]() ����t=2ʱ��S=6��
����t=2ʱ��S=6��
�ڵ�2��t��4ʱ����ͼ2����AP=AM+t=1+t����S=S��APQ=![]() AP��BC=
AP��BC=![]() ��1+t����4=2��t+1��=2t+2����t=4ʱ��S=8��
��1+t����4=2��t+1��=2t+2����t=4ʱ��S=8��
�۵�4��t��5ʱ����ͼ3���������CQ=t��4��PB=t+AM��AB=t+1��5=t��4����PQ=BC��CQ��PB=4����t��4������t��4��=12��2t����S=S��APQ=![]() PQ��AB=
PQ��AB=![]() ����12��2t����5=��5t+50����t=5ʱ��S=5��
����12��2t����5=��5t+50����t=5ʱ��S=5��
��S��t�ĺ�����ϵʽ�ֱ��Ǣ�S=S��APQ=![]() ����t=2ʱ��S=6����S=S��APQ=2t+2����t=4ʱ��S=8������S=S��APQ=��5t+50����t=5ʱ��S=5���ۺ��������������D��ȷ����ѡD��
����t=2ʱ��S=6����S=S��APQ=2t+2����t=4ʱ��S=8������S=S��APQ=��5t+50����t=5ʱ��S=5���ۺ��������������D��ȷ����ѡD��




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y��x2��x��1��x���һ������Ϊ(m��0)�������ʽm2��m��2017��ֵΪ____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ���У�������Գ�ͼ�ε��ǣ� ��
A.�߶�
B.��
C.����������
D.ֱ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ⷽ����Ļ���˼����_________��Ҳ���ǰѶ�Ԫһ�η�����ת��Ϊ______________�� ��Ԫ�ķ����У�_____________��_______________�ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�������������У�ÿ��С�����DZ߳�Ϊ1�������Σ�A��B������С����Ķ����ϣ�λ����ͼ��ʾ����CҲ��С����Ķ����ϣ�����A��B��CΪ����������ε����Ϊ1��ƽ����λ����C��ĸ���Ϊ�� ���� 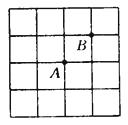
A.3��
B.4��
C.5��
D.6��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������һ�κ���y=��2x+5ͼ���������������� ��
��A��y��x���������С
��B��ֱ�߾�����һ������������
��C��ֱ�ߴ��������½���
��D��ֱ����x�ύ����������0��5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�����߾�������ԭ��O��x������һ��E������M������Ϊ��2��4��������ABCD�Ķ���A���O�غϣ�AD��AB�ֱ���x�ᡢy���ϣ���AD=2��AB=3��
��1���������������Ӧ�ĺ�����ϵʽ��
��2��������ABCD��ÿ��1����λ���ȵ��ٶȴ���ͼ��ʾ��λ����x�������������ƽ���ƶ���ͬʱһ����PҲ����ͬ���ٶȴӵ�A������B�����ƶ����������˶���ʱ��Ϊt�루0��t��3����ֱ��AB��������ߵĽ���ΪN����ͼ2��ʾ����
�ٵ�t=![]() ʱ���жϵ�P�Ƿ���ֱ��ME�ϣ���˵�����ɣ�
ʱ���жϵ�P�Ƿ���ֱ��ME�ϣ���˵�����ɣ�
������P��N��C��DΪ����Ķ�������ΪS������S�Ƿ�������ֵ�������ڣ����������ֵ���������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com