
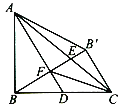
【题目】如图,点 D 是等腰直角 △ABC 腰 BC 上的中点,点B 、B′ 关于 AD 对称,且 BB′ 交AD 于 F,交 AC 于 E,连接 FC 、 AB′,下列说法:① ∠BAD=30°; ② ∠BFC=135°;③ AF=2B′ C;正确的个数是()
A. 1 B. 2 C. 3 D. 4
【答案】B
【解析】
依据点D是等腰直角△ABC腰BC上的中点,可得tan∠BAD=![]() ,即可得到∠BAD≠30°;连接B'D,即可得到∠BB'C=∠BB'D+∠DB'C=90°,进而得出△ABF≌△BCB',判定△FCB'是等腰直角三角形,即可得到∠CFB'=45°,即∠BFC=135°;由△ABF≌△BCB',可得AF=BB'=2BF=2B'C;依据△AEF与△CEB'不全等,即可得到S△AFE≠S△FCE.
,即可得到∠BAD≠30°;连接B'D,即可得到∠BB'C=∠BB'D+∠DB'C=90°,进而得出△ABF≌△BCB',判定△FCB'是等腰直角三角形,即可得到∠CFB'=45°,即∠BFC=135°;由△ABF≌△BCB',可得AF=BB'=2BF=2B'C;依据△AEF与△CEB'不全等,即可得到S△AFE≠S△FCE.
∵点D是等腰直角△ABC腰BC上的中点,
∴BD=![]() BC=
BC=![]() AB,
AB,
∴tan∠BAD=![]() ,
,
∴∠BAD≠30°,故①错误;
如图,连接B'D,
∵B、B′关于AD对称,
∴AD垂直平分BB',
∴∠AFB=90°,BD=B'D=CD,
∴∠DBB'=∠BB'D,∠DCB'=∠DB'C,
∴∠BB'C=∠BB'D+∠DB'C=90°,
∴∠AFB=∠BB'C,
又∵∠BAF+∠ABF=90°=∠CBB'+∠ABF,
∴∠BAF=∠CBB',
∴△ABF≌△BCB',
∴BF=CB'=B'F,
∴△FCB'是等腰直角三角形,
∴∠CFB'=45°,即∠BFC=135°,故②正确;
由△ABF≌△BCB',可得AF=BB'=2BF=2B'C,故③正确;
∵AF>BF=B'C,
∴△AEF与△CEB'不全等,
∴AE≠CE,
∴S△AFE≠S△FCE,故④错误;
故选B.


科目:初中数学 来源: 题型:
【题目】如图,△ABC经过一次平移到△DFE的位置,请回答下列问题:
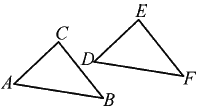
(1)点C的对应点是点__________,∠D=__________,BC=__________;
(2)连接CE,那么平移的方向就是__________的方向,平移的距离就是线段__________的长度;
(3)连接AD,BF,BE,与线段CE相等的线段有__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一组正方形按如图所示的方式放置,其中顶点B1在y轴上,顶点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…,则正方形A2017B2017C2017D2017的边长是( ) 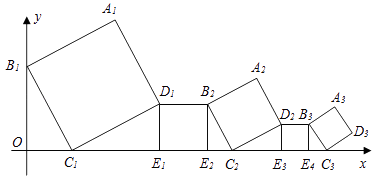
A.( ![]() )2016
)2016
B.( ![]() )2017
)2017
C.( ![]() )2016
)2016
D.( ![]() )2017
)2017
查看答案和解析>>
科目:初中数学 来源: 题型:
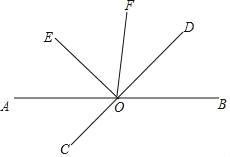
【题目】如图,直线AB、CD相交于点O,OE⊥OD,OE平分∠AOF.
(1)∠BOD与∠DOF相等吗?请说明理由.
(2)若∠DOF=![]() ∠BOE,求∠AOD的度数.
∠BOE,求∠AOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是小明家和学校所在地的简单地图,已知OA=2cm,OB=2.5cm,OP=4cm,点C为OP的中点,回答下列问题:
(1)图中距小明家距离相同的是哪些地方?
(2)学校、商场和停车场分别在小明家的什么方位?
(3)如果学校距离小明家400m,那么商场和停车场分别距离小明家多远?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△DEF的各顶点分别在双曲线y= ![]() ,y=
,y= ![]() ,y=
,y= ![]() 在第一象限的图象上,若∠C=∠F=90°,AC∥DF∥x轴,BC∥EF∥y轴,则S△ABC﹣S△DEF=( )
在第一象限的图象上,若∠C=∠F=90°,AC∥DF∥x轴,BC∥EF∥y轴,则S△ABC﹣S△DEF=( ) 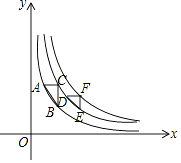
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
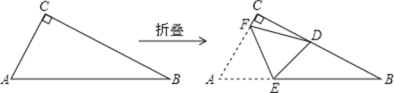
【题目】直角三角形纸片 ABC 中,∠ACB=90°,AC≤BC.如图,将纸片沿某条直线折叠,使点 A 落在直角边 BC 上,记落点为 D.设折痕与 AB、AC 边分别交于点 E、点 F,当折叠后的△CDF 与△BDE 均为等腰三角形,那么纸片中∠B 的度数是_____
查看答案和解析>>
科目:初中数学 来源: 题型:
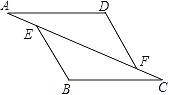
【题目】如图,已知:在△AFD和△CEB中,点A、E、F、C在同一直线上,AE=CF,∠B=∠D,AD∥BC.
(1)AD与BC相等吗?请说明理由;
(2)BE与DF平行吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com