
【题目】接下面各题
(1)解方程:x2+x﹣1=0
(2)抛物线y=﹣x2+bx+c经过点(1,0),(﹣3,0),求b、c的值.
【答案】
(1)解:a=1,b=1,c=﹣1,
△=b2﹣4ac=5,
则x= ![]() ,
,
x1= ![]() ,x2=
,x2= ![]()
(2)∵y=﹣x2+bx+c经过点(1,0),(﹣3,0),
∴ ![]() ,
,
解得 ![]()
【解析】(1)求出根的判别式,利用公式法求出方程的解;(2)利用待定系数法列出b和c的二元一次方程组,求出b和c的值即可.
【考点精析】关于本题考查的抛物线与坐标轴的交点,需要了解一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
(1)求证:△BED≌△CFD;
(2)若∠A=60°,BE=1,求△ABC的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y= ![]() x与反比例函数y=
x与反比例函数y= ![]() 在第一象限内的图象相交于点A(m,3).
在第一象限内的图象相交于点A(m,3).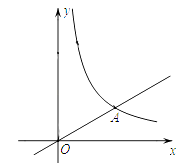
(1)求该反比例函数的关系式;
(2)将直线y= ![]() x沿y轴向上平移8个单位后与反比例函数在第一象限内的图象相交于点B,连接AB,这时恰好AB⊥OA,求tan∠AOB的值;
x沿y轴向上平移8个单位后与反比例函数在第一象限内的图象相交于点B,连接AB,这时恰好AB⊥OA,求tan∠AOB的值;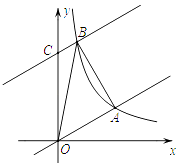
(3)在(2)的条件下,在射线OA上存在一点P,使△PAB∽△BAO,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点 D 是等腰直角 △ABC 腰 BC 上的中点,点B 、B′ 关于 AD 对称,且 BB′ 交AD 于 F,交 AC 于 E,连接 FC 、 AB′,下列说法:① ∠BAD=30°; ② ∠BFC=135°;③ AF=2B′ C;正确的个数是()
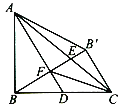
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
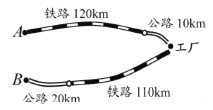
【题目】如图,某化工厂与A,B两地有公路和铁路相连,这家工厂从A地购买一批每吨1 000元的原料运回工厂,制成每吨8 000元的产品运到B地.已知公路运价为1.5元/(吨千米),铁路运价为1.2元/(吨千米),这两次运输共支出公路运费15 000元,铁路运费97 200元,请计算这批产品的销售款比原料费和运输费的和多多少元?
(1)根据题意,甲、乙两名同学分别列出尚不完整的方程组如下:
甲:![]()
乙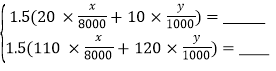 :
:
根据甲,乙两名同学所列方程组,请你分别指出未知数x,y表示的意义,然后在等式右边补全甲、乙两名同学所列方程组.
甲:x表示 ,y表示 ;
乙:x表示 ,y表示 .
(2)甲同学根据他所列方程组解得x=300,请你帮他解出y的值,并解决该实际问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列一元一次方程解应用题:
2018年是我国改革开放40周年,改革开放是当代中国发展进步的必由之路,是实现中国梦的必由之路. 2018年10月20日在国家大剧院举行了《可爱的中国》庆祝改革开放40周年音乐会. 本次演出的票价分为以下几个类别,如下表所示:
演出票类别 | A类 | B类 | C类 | D类 | E类 |
演出票单价(元/张) | 300 | 280 | 240 | 180 | 100 |
小宇购买了A类和C类的演出票共10张,他发现这10张演出票的总价恰好可以购买8张B类票和4张E类票. 问小宇购买A类和C类的演出票各几张?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
国际比赛的足球场长在100m到110m之间,宽在64m到75m之间,为了迎接2015年的亚洲杯,某地建设了一个长方形的足球场,其长是宽的1.5倍,面积是7560m2.请你判断这个足球场能用于国际比赛吗?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC⊥BC,C为垂足,CD⊥AB,D为垂足,BC=8,CD=4.8,BD=6.4,AD=3.6,AC= 6,那么点C到AB的距离是_______,点A到BC的距离是________,点B到CD 的距离是_____,A、B两点的距离是_________.
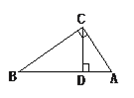
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com