
����Ŀ����֪��ԭ��O����ֱ����Բ��ΪM��0��4�����뾶Ϊ2��Բ���У��е�ֱ�ΪP��Q��PQ��y���ڵ�K�������߾���P��Q���㣬����ΪN��0��6��������x�ύ��A��B���㣮 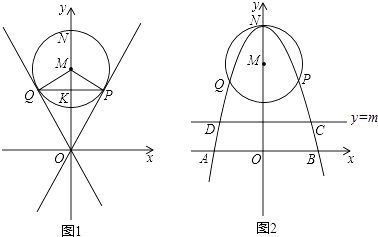
��1�����P�����ꣻ
��2���������߽���ʽ��
��3����ֱ��y=nx+m�У���n=0��m��0ʱ��y=m��ƽ����x���ֱ�ߣ���ֱ��y=m���������ཻ�ڵ�C��D������ֱ�����M����ʱ�����A��B��C��DΧ�ɵĶ���ε����������������ţ���
���𰸡�
��1���⣺��ͼ1��
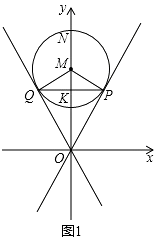
�ߡ�M��OP�����ڵ�P��
��MP��OP������MPO=90�㣮
�ߵ�M��0��4����OM=4��MP=2��
��OP=2 ![]() ��
��
�ߡ�M��OP�����ڵ�P����M��OQ�����ڵ�Q��
��OQ=OP����POK=��QOK��
��OK��PQ��QK=PK��
��PK= ![]() =
= ![]() =
= ![]() ��
��
��OK= ![]() =3��
=3��
���P�������� ![]() ��3��
��3��
��2���⣺��ͼ2��

�趥��Ϊ��0��6���������ߵĽ���ʽΪy=ax2+6��
�ߵ�P�� ![]() ��3����������y=ax2+6�ϣ�
��3����������y=ax2+6�ϣ�
��3a+6=3��
��ã�a=��1��
��������ߵĽ���ʽΪy=��x2+6
��3���⣺��ֱ��y=m���M����ʱ��
���� ![]() =2��
=2��
��ã�m1=2��m2=6��
��m=2ʱ����ͼ3��
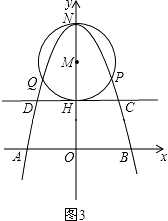
����OH=2��
��y=2ʱ���ⷽ�̩�x2+6=2�ã�x=��2��
���C��2��2����D����2��2����CD=4��
ͬ���ɵã�AB=2 ![]() ��
��
��S����ABCD= ![]() ��DC+AB��OH=
��DC+AB��OH= ![]() ��4+2
��4+2 ![]() ����2=4+2
����2=4+2 ![]() ��
��
��m=6ʱ����ͼ4��

��ʱ��C����D���N�غϣ�
S��ABC= ![]() ABOC=
ABOC= ![]() ��2
��2 ![]() ��6=6
��6=6 ![]() ��
��
������������A��B��C��DΧ�ɵĶ���ε����Ϊ4+2 ![]() ��6
��6 ![]()
����������1�������ߵ����ʿɵá�MPO=90�㣬���ݹ��ɶ��������PO��Ȼ��������������PK��Ȼ�����ù��ɶ��������OK���Ϳɵõ���P�����꣮��2�����趥��Ϊ��0��6���������ߵĽ���ʽΪy=ax2+6��Ȼ��P���������Ϳ���������ߵĽ���ʽ����3��ֱ��y=m���M���������ֿ��ܣ�ֻ�������������ֱ����۾Ϳ������Ӧ����ε������
�����㾫����ͨ������������߳������͵��������ε����ʣ����մ�Բ��һ����Բ���������ߣ����ǵ����߳����Բ�ĺ���һ�������ƽ���������ߵļнǣ����������ε���������ȣ���ƣ��ȱ߶ԵȽǣ������Խ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ij�����꼶ѧ���������������������ȫ�����꼶ѧ���������ȡ�˲���ѧ��������һ���������Կ�Ŀ���ԣ��Ѳ��Խ����Ϊ�ĸ��ȼ���A�������㣺B�������ã�C��������D�����������������Խ���������ͼ������������ͳ��ͼ�������ͳ��ͼ�е���Ϣ����������⣺ 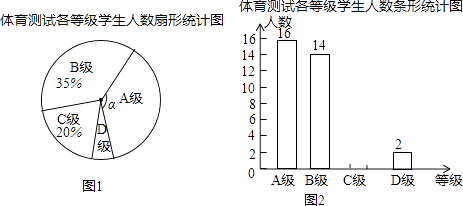
��1�����γ������Ե�ѧ������
��2����ͼ1�СϦ��Ķ������㣬
��3����ͼ2����ͳ��ͼ����������
��4���������꼶��ѧ��3500�������ȫ���μ����������Ŀ���ԣ�����Ʋ����������Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ��֪��ABC�У���A=25�㣬��B=40�㣮 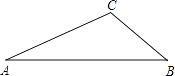
��1����������O��ʹ�á�O����A��C���㣬��Բ��O����AB���ϣ���Ҫ��߹���ͼ��������ͼ�ۼ�������д������
��2����֤��BC�ǣ�1����������O�����ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��E��F���ı���ABCD�ĶԽ����ӳ����ϣ�AE=CF��DE��BF����1=��2�� 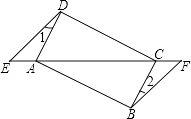
��1����֤����AED�ա�CFB��
��2����AD��CD���ı���ABCD��ʲô�����ı��Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��E��F���ı���ABCD�ĶԽ����ӳ����ϣ�AE=CF��DE��BF����1=��2�� 
��1����֤����AED�ա�CFB��
��2����AD��CD���ı���ABCD��ʲô�����ı��Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����y=ax+b������1��3������0����2������a��b=�� ��
A.��1
B.��3
C.3
D.7
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ѡ����Ŀͳ��ͼ
��Ŀ | Ƶ�� | Ƶ�� |
A | 80 | b |
B | c | 0.3 |
C | 20 | 0.1 |
D | 40 | 0.2 |
�ϼ� | a | 1 |
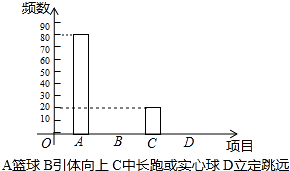
��1���������a��b��c��ֵ����������ͳ��ͼ���������� ����a= �� b= �� c= ��
��2�������3���˲μ�����ѡ�������ж�����ѡ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪A����4�� ![]() ����B����1��2����һ�κ���y=kx+b�뷴��������y=
����B����1��2����һ�κ���y=kx+b�뷴��������y= ![]() ��m��0��x��0��ͼ����������㣬AC��x����C��BD��y����D��
��m��0��x��0��ͼ����������㣬AC��x����C��BD��y����D�� 
��1������ͼ��ֱ�ӻش��ڵڶ������ڣ���xȡ��ֵʱ��һ�κ������ڷ�����������ֵ��
��2����һ�κ�������ʽ��m��ֵ��
��3��P���߶�AB�ϵ�һ�㣬����PC��PD������PCA�͡�PDB�����ȣ����P���꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ĸ������壺
��������ͼ�븩��ͼ��ͬ�ļ����干�У�������
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com