
【题目】如图,已知点E、F在四边形ABCD的对角线延长线上,AE=CF,DE∥BF,∠1=∠2. 
(1)求证:△AED≌△CFB;
(2)若AD⊥CD,四边形ABCD是什么特殊四边形?请说明理由.
【答案】
(1)证明:∵DE∥BF,
∴∠E=∠F,
在△AED和△CFB中,
 ,
,
∴△AED≌△CFB(AAS)
(2)解:四边形ABCD是矩形.
理由如下:∵△AED≌△CFB,
∴AD=BC,∠DAE=∠BCF,
∴∠DAC=∠BCA,
∴AD∥BC,
∴四边形ABCD是平行四边形,
又∵AD⊥CD,
∴四边形ABCD是矩形
【解析】(1)根据两直线平行,内错角相等可得∠E=∠F,再利用“角角边”证明△AED和△CFB全等即可;(2)根据全等三角形对应边相等可得AD=BC,∠DAE=∠BCF,再求出∠DAC=∠BCA,然后根据内错角相等,两直线平行可得AD∥BC,再根据一组对边平行且相等的四边形是平行四边形证明四边形ABCD是平行四边形,再根据有一个角是直角的平行四边形是矩形解答.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠CAB=65°,在同一平面内,将△ABC绕点A旋转到△AED的位置,使得DC∥AB,则∠BAE等于( ) 
A.30°
B.40°
C.50°
D.60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有2条生产线计划在一个月(30天)内组装520台产品(每天产品的产量相同),按原先的组装速度,不能完成任务;若加班生产,每条生产线每天多组装2台产品,能提前完成任务.
(1)每条生产线原先每天最多能组装多少台产品?
(2)要按计划完成任务,策略一:增添1条生产线,共要多投资19000元;策略二:按每天能组装最多台数加班生产,每条生产线每天共要多花费350元;选哪一个策略较省费用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知过原点O的两直线与圆心为M(0,4),半径为2的圆相切,切点分别为P、Q,PQ交y轴于点K,抛物线经过P、Q两点,顶点为N(0,6),且与x轴交于A、B两点. 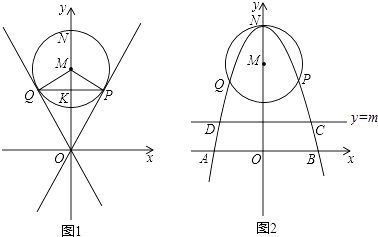
(1)求点P的坐标;
(2)求抛物线解析式;
(3)在直线y=nx+m中,当n=0,m≠0时,y=m是平行于x轴的直线,设直线y=m与抛物线相交于点C、D,当该直线与⊙M相切时,求点A、B、C、D围成的多边形的面积(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c图象如图,下列正确的个数为( )
①bc>0;
②2a﹣3c<0;
③2a+b>0;
④ax2+bx+c=0有两个解x1 , x2 , 当x1>x2时,x1>0,x2<0;
⑤a+b+c>0;
⑥当x>1时,y随x增大而减小.
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( ) 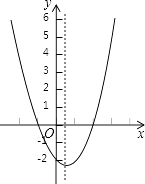
A.函数有最小值
B.对称轴是直线x= ![]()
C.当x< ![]() ,y随x的增大而减小
,y随x的增大而减小
D.当﹣1<x<2时,y>0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若z=3x(3y﹣x)﹣(4x﹣3y)(x+3y)
(1)若x,y均为整数,求证:当x是3的倍数时,z能被9整除;
(2)若y=x+1,求z的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com