
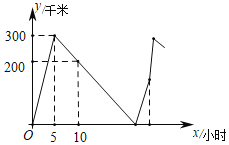
【题目】已知A、B、C三地顺次在同一直线上,A、C两地相距1400千米,甲乙两车均从A地出发,向B地方向匀速前进,甲车出发5小时后,乙车出发,经过一段时间后两车在B地相遇,甲车到达B地后便在B地卸货,卸完货后从B地按原车速的![]() 返回A地,而乙车到B地后立刻继续以原速前往C地,到达C地后按原车速的
返回A地,而乙车到B地后立刻继续以原速前往C地,到达C地后按原车速的![]() 原路返回A地,结果甲乙两车同时返回A地,若两车间的距离y(千米)与甲车出发时间x(小时)之间的关系如图所示,则甲车在B地卸货用了_____小时.
原路返回A地,结果甲乙两车同时返回A地,若两车间的距离y(千米)与甲车出发时间x(小时)之间的关系如图所示,则甲车在B地卸货用了_____小时.
【答案】1.5
【解析】
根据题意可得甲、乙两车原来的速度,根据两车在B地相遇,列方程即可求出A、B两地的距离,再次根据“路程=速度×时间”即可解答.
解:根据题意得:
甲车原来的的速度为:300÷5=60(千米/时),
乙车原来的的速度为:(60×10﹣200)÷(10﹣5)=80(千米/时),
设甲车出发x小时后得到B地,根据题意得:
60x=80(x﹣5),
解得x=20,
所以A、B两地的距离为:60×20=1200(千米),
所以B、C两地的距离为:1400﹣1200=200(千米),
乙车前往C地和返回A地所用时间为:200÷80+1400÷(80×![]() )=16.5(小时),
)=16.5(小时),
所以甲车在B地卸货所用时间为:16.5﹣1200÷(60×![]() )=1.5(小时).
)=1.5(小时).
故答案为:1.5


科目:初中数学 来源: 题型:
【题目】为支持国家南水北调工程建设,小王家由原来养殖户变为种植户,经市场调查得知,当种植樱桃的面积x不超过15亩时,每亩可获得利润y=1900元;超过15亩时,每亩获得利润y(元)与种植面积x(亩)之间的函数关系如下表(为所学过的一次函数,反比例函数或二次函数中的一种)
x(亩) | 20 | 25 | 30 | 35 |
y(元) | 1800 | 1700 | 1600 | 1500 |
(1)请求出种植樱桃的面积超过15亩时每亩获得利润y与x的函数关系式;
(2)如果小王家计划承包荒山种植樱桃,受条件限制种植樱桃面积x不超过50亩,设小王家种植x亩樱桃所获得的总利润为W元,求小王家承包多少亩荒山获得的总利润最大,并求总利润W(元)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,楼房BD的前方竖立着旗杆AC.小亮在B处观察旗杆顶端C的仰角为45°,在D处观察旗杆顶端C的俯角为30°,楼高BD为20米.
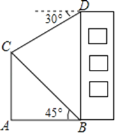
(1)求∠BCD的度数;
(2)求旗杆AC的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+2x+c(a<0)与x轴交于点A和点B(点A在原点的左侧,点B在原点的右侧),与y轴交于点C,OB=OC=3.
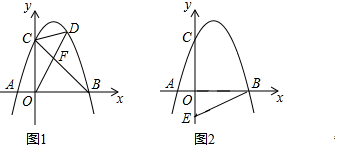
(1)求该抛物线的函数解析式;
(2)如图1,连接BC,点D是直线BC上方抛物线上的点,连接OD,CD,OD交BC于点F,当S△COF:S△CDF=3:2时,求点D的坐标.
(3)如图2,点E的坐标为(0,![]() ),在抛物线上是否存在点P,使∠OBP=2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.
),在抛物线上是否存在点P,使∠OBP=2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,是真命题的是( )
A.将函数y=![]() x+1向右平移2个单位后所得函数的解析式为y=
x+1向右平移2个单位后所得函数的解析式为y=![]() x
x
B.若一个数的平方根等于其本身,则这个数是0和1
C.对函数y=![]() ,其函数值y随自变量x的增大而增大
,其函数值y随自变量x的增大而增大
D.直线y=3x+1与直线y=﹣3x+2一定互相平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x函数y=|﹣x2+bx﹣7|﹣4,点(4,5)在函数上,且b为整数,根据我们已有的研究函数的经验,请对该函数及其图象进行如下探究,并完成以下问题:
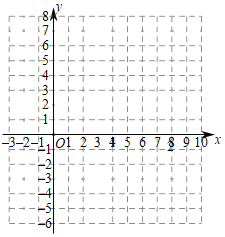
(1)求b= ;
(2)函数图象探究:
①下表是y与x的几组对应值,请直接写出m与n的值:m= ,n= ;
x | … | ﹣ | 0 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 7 | 8 | 8 | … |
y | … | m | 3 |
| ﹣4 | 1 | 4 | n | 4 | 1 | ﹣4 |
| 3 | 5 | … |
②根据你喜欢的方式,在如图所示的平面直角坐标系中,画出该函数图象;
(3)结果函数图象,写出该函数的一条性质: ;
(4)若关于x的方程|﹣x2+bx﹣7|=m+4有四个根,则m的取值范围为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 为等腰直角三角形,∠ACB=90°,点 M 为 AB 边的中点,点 N 为射线 AC 上一点,连接 BN,过点 C 作 CD⊥BN 于点 D,连接 MD,作∠BNE=∠BNA,边 EN 交射线 MD 于点 E,若 AB=20![]() ,MD=14
,MD=14![]() ,则 NE 的长为___.
,则 NE 的长为___.
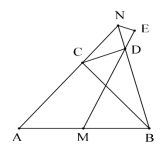
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列6×6的网格中,横、纵坐标均A(0,3),B(5,3)、C(1,5)都是格点在网格中仅用无刻度的直尺作图,保留作图痕迹.
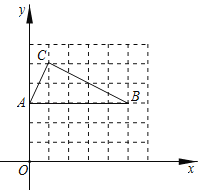
(1)画出以AB为斜边的等腰Rt△ABD(D在AB下方);
(2)连接CD交AB于点E,则∠ACE的度数为 ;
(3)在直线AB下方找一个格点F,连接CF,使∠ACF=∠AEC,直接写出F点坐标 ;
(4)由上述作图直接写出tan∠AEC的值 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车相遇后都停下来休息,快车休息2个小时后,以原速的![]() 继续向甲行驶,慢车休息3小时后,接到紧急任务,以原速的
继续向甲行驶,慢车休息3小时后,接到紧急任务,以原速的![]() 返回甲地,结果快车比慢车早2.25小时到达甲地,两车之间的距离S(千米)与慢车出发的时间t(小时)的函数图象如图所示,则当快车到达甲地时,慢车距乙地______千米.
返回甲地,结果快车比慢车早2.25小时到达甲地,两车之间的距离S(千米)与慢车出发的时间t(小时)的函数图象如图所示,则当快车到达甲地时,慢车距乙地______千米.
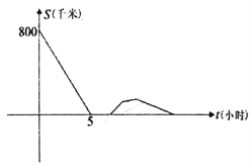
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com