
ЁОЬтФПЁПвбжЊЙигкxКЏЪ§yЃН|Љx2+bxЉ7|Љ4ЃЌЕуЃЈ4ЃЌ5ЃЉдкКЏЪ§ЩЯЃЌЧвbЮЊећЪ§ЃЌИљОнЮвУЧвбгаЕФбаОПКЏЪ§ЕФОбщЃЌЧыЖдИУКЏЪ§МАЦфЭМЯѓНјааШчЯТЬНОПЃЌВЂЭъГЩвдЯТЮЪЬтЃК
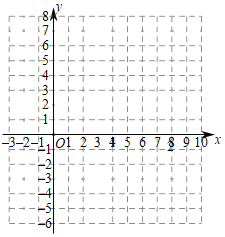
ЃЈ1ЃЉЧѓbЃНЁЁ ЁЁЃЛ
ЃЈ2ЃЉКЏЪ§ЭМЯѓЬНОПЃК
ЂйЯТБэЪЧyгыxЕФМИзщЖдгІжЕЃЌЧыжБНгаДГіmгыnЕФжЕЃКmЃНЁЁ ЁЁЃЌnЃНЁЁ ЁЁЃЛ
x | Ё | Љ | 0 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 7 | 8 | 8 | Ё |
y | Ё | m | 3 |
| Љ4 | 1 | 4 | n | 4 | 1 | Љ4 |
| 3 | 5 | Ё |
ЂкИљОнФуЯВЛЖЕФЗНЪНЃЌдкШчЭМЫљЪОЕФЦНУцжБНЧзјБъЯЕжаЃЌЛГіИУКЏЪ§ЭМЯѓЃЛ
ЃЈ3ЃЉНсЙћКЏЪ§ЭМЯѓЃЌаДГіИУКЏЪ§ЕФвЛЬѕаджЪЃКЁЁ ЁЁЃЛ
ЃЈ4ЃЉШєЙигкxЕФЗНГЬ|Љx2+bxЉ7|ЃНm+4гаЫФИіИљЃЌдђmЕФШЁжЕЗЖЮЇЮЊЁЁ ЁЁЃЎ
ЁОД№АИЁПЃЈ1ЃЉ8ЃЛЃЈ2ЃЉЂй![]() ЃЌ5ЃЛЂкМћНтЮіЃЛЃЈ3ЃЉКЏЪ§ЙигкxЃН4ЖдГЦЃЛЃЈ4ЃЉЉ4ЃМmЃМ5.
ЃЌ5ЃЛЂкМћНтЮіЃЛЃЈ3ЃЉКЏЪ§ЙигкxЃН4ЖдГЦЃЛЃЈ4ЃЉЉ4ЃМmЃМ5.
ЁОНтЮіЁП
ЃЈ1ЃЉНЋЕуЃЈ4ЃЌ5ЃЉДњШыКЏЪ§yЃН|Љx2+bxЉ7|Љ4ЃЌНсКЯbЪЧећЪ§ЕФЬѕМўМДПЩЧѓНтЃЛ
ЃЈ2ЃЉЂйгЩyЃН|Љx2+8xЉ7|Љ4ЃЌЕБxЃНЉ![]() ЪБЃЌyЃН
ЪБЃЌyЃН![]() ЃЛЕБxЃН4ЪБЃЌyЃН5ЃЛдђгаmЃН
ЃЛЕБxЃН4ЪБЃЌyЃН5ЃЛдђгаmЃН![]() ЃЌnЃН5ЃЛЂкУшЕуЗЈЛЭММДПЩЃЛ
ЃЌnЃН5ЃЛЂкУшЕуЗЈЛЭММДПЩЃЛ
ЃЈ3ЃЉКЏЪ§ЙигкxЃН4ЖдГЦЃЛЃЈаДГівЛЬѕМДПЩЃЉ
ЃЈ4ЃЉНсКЯЭМЯѓевЃЌЕБxЃН4ЪБЃЌyЃН5ЃЛЕБxЃН1ЃЌxЃН7ЪБЃЌyЃНЉ4ЃЛдђЕБЉ4ЃМmЃМ5ЪБЃЌ|Љx2+8xЉ7|ЃНm+4гаЫФИіИљЃЎ
НтЃКЃЈ1ЃЉНЋЕуЃЈ4ЃЌ5ЃЉДњШыКЏЪ§yЃН|Љx2+bxЉ7|Љ4ЃЌ
ЁрbЃН8ЛђbЃН3ЃЎ5ЃЌ
ЁпbЮЊећЪ§ЃЌ
ЁрbЃН8ЃЌ
ЙЪД№АИЮЊ8ЃЛ
ЃЈ2ЃЉЂйЁпbЃН8ЃЌ
ЁрyЃН|Љx2+8xЉ7|Љ4ЃЌ
ЕБxЃНЉ![]() ЪБЃЌyЃН
ЪБЃЌyЃН![]() ЃЛ
ЃЛ
ЕБxЃН4ЪБЃЌyЃН5ЃЛ
ЁрmЃН![]() ЃЌnЃН5ЃЌ
ЃЌnЃН5ЃЌ
ЙЪД№АИЮЊ![]() ЃЌ5ЃЛ
ЃЌ5ЃЛ
ЂкШчЭМЫљЪОЃК
ЃЈ3ЃЉКЏЪ§ЙигкxЃН4ЖдГЦЃЛ
ЃЈ4ЃЉЕБxЃН4ЪБЃЌyЃН5ЃЛ
ЕБxЃН1ЃЌxЃН7ЪБЃЌyЃНЉ4ЃЛ
ЁрЕБЉ4ЃМmЃМ5ЪБЃЌ|Љx2+8xЉ7|ЃНm+4гаЫФИіИљЃЌ
ЙЪД№АИЮЊЉ4ЃМmЃМ5ЃЎ



 ЬсЗжАйЗжАйМьВтОэЕЅдЊЦкФЉВтЪдОэЯЕСаД№АИ
ЬсЗжАйЗжАйМьВтОэЕЅдЊЦкФЉВтЪдОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
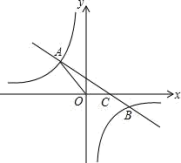
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§yЃНkx+bЃЈkЁй0ЃЉЕФЭМЯѓгыЗДБШР§КЏЪ§![]() ЕФЭМЯѓНЛгкЖўЁЂЫФЯѓЯоФкЕФAЁЂBСНЕуЃЌгыxжсНЛгкCЕуЃЌЕуAЕФзјБъЮЊЃЈЉ2ЃЌ3ЃЉЃЌЕуBЕФзјБъЮЊЃЈ4ЃЌnЃЉЃЎ
ЕФЭМЯѓНЛгкЖўЁЂЫФЯѓЯоФкЕФAЁЂBСНЕуЃЌгыxжсНЛгкCЕуЃЌЕуAЕФзјБъЮЊЃЈЉ2ЃЌ3ЃЉЃЌЕуBЕФзјБъЮЊЃЈ4ЃЌnЃЉЃЎ
ЃЈ1ЃЉЧѓИУЗДБШР§КЏЪ§КЭвЛДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉдкxжсЩЯЪЧЗёДцдкЕуPЃЌЪЙЁїAPCЪЧжБНЧШ§НЧаЮЃПШєДцЃЌЧѓГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫМѕЩйЮэіВЕФЧжзДЃЌФГЪаЛЗБЃОжгыЪаЮЏИїВПУХаЩЬЃЌвЊЧѓЪаУёдкДКНкЦкМфНћжЙШМЗХбЬЛЈБЌжёЃЌЮЊСЫеїМЏЪаУёЖдНћШМЕФвтМћЃЌеўИЎАьЙЋЪвНјааСЫГщбљЕїВщЃЌЕїВщвтМћБэЩшМЦЮЊЃКЁАТњвтЁАЁАвЛАуЁБЁБЮоЫљЮНЁБЁБЗДЖдЁБЫФИібЁЯюЃЌЕїВщНсЙћЛузмжЦГЩШчЯТВЛЭъећЕФЭГМЦЭМЃЌЧыИљОнЬсЙЉЕФаХЯЂНтД№ЯТУцЕФЮЪЬтЃЎ
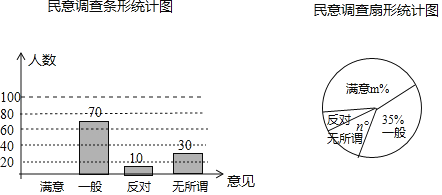
(1)ВЮгыЮЪОэЕїВщЕФШЫЪ§ЮЊЁЁ ЁЁЃЎ
(2)ЩШаЮЭГМЦЭМжаЕФmЃНЁЁ ЁЁЃЌnЃНЁЁ ЁЁЃЎВЙШЋЬѕаЮЭГМЦЭМЃЛ
(3)ШєБОЪаДКНкЦкМфСєЪиЪаЧјЕФЪаУёга32000ШЫЃЌЧыФуЙРМЦЫћУЧжаГжЁАЗДЖдЁБвтМћЕФШЫЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЮЊАыдВOЕФжБОЖЃЌЕуCдкАыдВЩЯЃЌЙ§ЕуOзїBCЕФЦНааЯпНЛACгкЕуEЃЌНЛЙ§ЕуAЕФжБЯпгкЕуDЃЌЧвЁЯD=ЁЯBAC
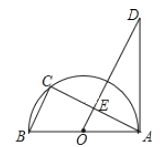
ЃЈ1ЃЉЧѓжЄЃКADЪЧАыдВOЕФЧаЯпЃЛ
ЃЈ2ЃЉЧѓжЄЃКЁїABCЁзЁїDOAЃЛ
ЃЈ3ЃЉШєBC=2ЃЌCE=![]() ЃЌЧѓADЕФГЄЃЎ
ЃЌЧѓADЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
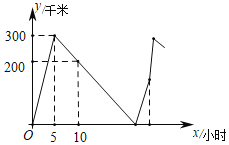
ЁОЬтФПЁПвбжЊAЁЂBЁЂCШ§ЕиЫГДЮдкЭЌвЛжБЯпЩЯЃЌAЁЂCСНЕиЯрОр1400ЧЇУзЃЌМзввСНГЕОљДгAЕиГіЗЂЃЌЯђBЕиЗНЯђдШЫйЧАНјЃЌМзГЕГіЗЂ5аЁЪБКѓЃЌввГЕГіЗЂЃЌОЙ§вЛЖЮЪБМфКѓСНГЕдкBЕиЯргіЃЌМзГЕЕНДяBЕиКѓБудкBЕиаЖЛѕЃЌаЖЭъЛѕКѓДгBЕиАДдГЕЫйЕФ![]() ЗЕЛиAЕиЃЌЖјввГЕЕНBЕиКѓСЂПЬМЬајвддЫйЧАЭљCЕиЃЌЕНДяCЕиКѓАДдГЕЫйЕФ
ЗЕЛиAЕиЃЌЖјввГЕЕНBЕиКѓСЂПЬМЬајвддЫйЧАЭљCЕиЃЌЕНДяCЕиКѓАДдГЕЫйЕФ![]() дТЗЗЕЛиAЕиЃЌНсЙћМзввСНГЕЭЌЪБЗЕЛиAЕиЃЌШєСНГЕМфЕФОрРыyЃЈЧЇУзЃЉгыМзГЕГіЗЂЪБМфxЃЈаЁЪБЃЉжЎМфЕФЙиЯЕШчЭМЫљЪОЃЌдђМзГЕдкBЕиаЖЛѕгУСЫ_____аЁЪБЃЎ
дТЗЗЕЛиAЕиЃЌНсЙћМзввСНГЕЭЌЪБЗЕЛиAЕиЃЌШєСНГЕМфЕФОрРыyЃЈЧЇУзЃЉгыМзГЕГіЗЂЪБМфxЃЈаЁЪБЃЉжЎМфЕФЙиЯЕШчЭМЫљЪОЃЌдђМзГЕдкBЕиаЖЛѕгУСЫ_____аЁЪБЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁдЊВНааДгМвШЅЛ№ГЕеОЃЌзпЕН 6 ЗжжгЪБЃЌвдЭЌбљЕФЫйЖШЛиМвШЁЮяЦЗЃЌШЛКѓДгМвГЫГізтГЕИЯЭљЛ№ГЕеОЃЌНсЙћБШдЄМЦВНааЪБМфЬсЧАСЫ3 ЗжжгЃЎаЁдЊРыМвТЗГЬS(Уз)гыЪБМфt(Зжжг)жЎМфЕФКЏЪ§ЭМЯѓШчЭМЃЌДгМвЕНЛ№ГЕеОТЗГЬЪЧ( )

A.1300 УзB.1400 УзC.1600 УзD.1500 Уз
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКЫФБпаЮ ABCD ФкНггкЁбOЃЌСЌНг ACЁЂBDЃЌЁЯBAD+2ЁЯACB=180ЁуЃЎ
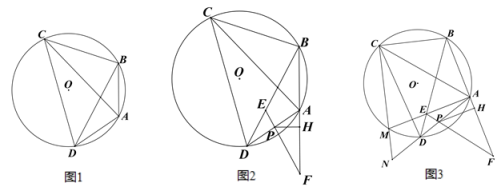
ЃЈ1ЃЉШчЭМ 1ЃЌЧѓжЄЃКЕу A ЮЊЛЁ BD ЕФжаЕуЃЛ
ЃЈ2ЃЉШчЭМ 2ЃЌЕу E ЮЊЯв BD ЩЯвЛЕуЃЌбгГЄ BA жСЕу FЃЌЪЙЕУ AF=ABЃЌСЌНг FE НЛ AD гкЕу PЃЌЙ§Еу P зї PHЁЭAF гкЕу HЃЌAF=2AH+APЃЌЧѓжЄЃКAH:AB=PE:BEЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌШчЭМ 3ЃЌСЌНг AEЃЌВЂбгГЄ AE НЛЁбO гкЕу MЃЌСЌНг CMЃЌВЂбгГЄ CM НЛ AD ЕФбгГЄЯпгкЕу NЃЌСЌНг FDЃЌЁЯMND=ЁЯMEDЃЌDF=12ЉqsinЁЯACBЃЌMN=![]() ЃЌЧѓ AH ЕФГЄЃЎ
ЃЌЧѓ AH ЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊШёНЧЁЯAOBШчЭМЃЌЃЈ1ЃЉдкЩфЯпOAЩЯШЁвЛЕуCЃЌвдЕуOЮЊдВаФЃЌOCГЄЮЊАыОЖзї![]() ЃЌНЛЩфЯпOBгкЕуDЃЌСЌНгCDЃЛ
ЃЌНЛЩфЯпOBгкЕуDЃЌСЌНгCDЃЛ
ЃЈ2ЃЉЗжБ№вдЕуCЃЌDЮЊдВаФЃЌCDГЄЮЊАыОЖзїЛЁЃЌНЛ![]() гкЕуMЃЌNЃЛ
гкЕуMЃЌNЃЛ
ЃЈ3ЃЉСЌНгOMЃЌMNЃЎ
ИљОнвдЩЯзїЭМЙ§ГЬМАЫљзїЭМаЮЃЌЯТСаНсТлжаДэЮѓЕФЪЧЃЈ ЃЉ

A. ЁЯCOM=ЁЯCODB. ШєOM=MNЃЌдђЁЯAOB=20Ёу
C. MNЁЮCDD. MN=3CD
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
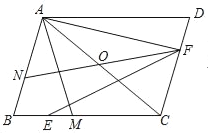
ЁОЬтФПЁПШчЭМЃЌЦНааЫФБпаЮABCDжаЃЌЕуOЪЧЖдНЧЯпACЕФжаЕуЃЌЕуMЮЊBCЩЯвЛЕуЃЌСЌНгAMЃЌЧвAB=AMЃЌЕуEЮЊBMжаЕуЃЌAFЁЭABЃЌСЌНгEFЃЌбгГЄFOНЛABгкЕуNЃЎ
ЃЈ1ЃЉШєBM=4ЃЌMC=3ЃЌAC=![]() ЃЌЧѓAMЕФГЄЖШЃЛ
ЃЌЧѓAMЕФГЄЖШЃЛ
ЃЈ2ЃЉШєЁЯACB=45ЁуЃЌЧѓжЄЃКAN+AF=![]() EFЃЎ
EFЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com