
【题目】如图,AB为半圆O的直径,点C在半圆上,过点O作BC的平行线交AC于点E,交过点A的直线于点D,且∠D=∠BAC
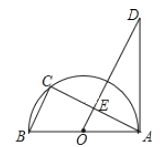
(1)求证:AD是半圆O的切线;
(2)求证:△ABC∽△DOA;
(3)若BC=2,CE=![]() ,求AD的长.
,求AD的长.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)要证AD是半圆O的切线只要证明∠DAO=90°即可;
(2)根据两组角对应相等的两个三角形相似即可得证;
(3)先求出AC、AB、AO的长,由第(2)问的结论△ABC∽△DOA,根据相似三角形的性质:对应边成比例可得到AD的长.
(1)证明:∵AB为直径,
∴∠ACB=90°,
又∵OD∥BC,
∴∠AEO=∠ACB=90°,
∴∠AOD+∠BAC=90°,
又∵∠D=∠BAC,
∴∠AOD+∠D=90°,
∴∠OAD=90°,
∴AD⊥OA,
∴AD是半圆O的切线;
(2)证明:由(1)得∠ACB=∠OAD=90°,
又∵∠D=∠BAC,
∴△ABC∽△DOA;
(3)解:∵O为AB中点,OD∥BC,
∴OE是△ABC的中位线,则E为AC中点,
∴AC=2CE,
∵BC=2,CE=![]() ,
,
∴AC=![]()
∴AB=![]() ,
,
∴OA=![]() AB=
AB=![]() ,
,
由(2)得:△ABC∽△DOA,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源: 题型:
【题目】已知∠MON=120°,点A,B分别在ON,OM边上,且OA=OB,点C在线段OB上(不与点O,B重合),连接CA.将射线CA绕点C逆时针旋转120°得到射线CA′,将射线BO绕点B逆时针旋转150°与射线CA′交于点D.

(1)根据题意补全图1;
(2)求证:
①∠OAC=∠DCB;
②CD=CA(提示:可以在OA上截取OE=OC,连接CE);
(3)点H在线段AO的延长线上,当线段OH,OC,OA满足什么等量关系时,对于任意的点C都有∠DCH=2∠DAH,写出你的猜想并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业为响应国家教育扶贫的号召,决定对某乡镇全体贫困初、高中学生进行资助,初中学生每月资助200元,高中学生每月资助300元.已知该乡受资助的初中学生人数是受资助的高中学生人数的2倍,且该企业在2018年下半年7﹣12月这6个月资助学生共支出10.5万元.
(1)问该乡镇分别有多少名初中学生和高中学生获得了资助?
(2)2018年7﹣12月期间,受资助的初、高中学生中,分别有30%和40%的学生被评为优秀学生,从而获得了该乡镇政府的公开表扬.同时,提供资助的企业为了激发更多受资助学生的进取心和学习热情,决定对2019年上半年1﹣6月被评为优秀学生的初中学生每人每月增加a%的资助,对被评为优秀学生的高中学生每人每月增加2a%的资助.在此奖励政策的鼓励下,2019年1﹣6月被评为优秀学生的初、高中学生分別比2018年7﹣12月的人数增加了3a%、a%.这样,2019年上半年评为优秀学生的初、高中学生所获得的资助总金额一个月就达到了10800元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
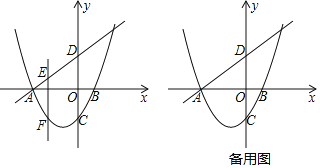
【题目】如图,抛物线y=ax2+bx﹣1(a≠0)交x轴于A,B(1,0)两点,交y轴于点C,一次函数y=x+3的图象交坐标轴于A,D两点,E为直线AD上一点,作EF⊥x轴,交抛物线于点F
(1)求抛物线的解析式;
(2)若点F位于直线AD的下方,请问线段EF是否有最大值?若有,求出最大值并求出点E的坐标;若没有,请说明理由;
(3)在平面直角坐标系内存在点G,使得G,E,D,C为顶点的四边形为菱形,请直接写出点G的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+2x+c(a<0)与x轴交于点A和点B(点A在原点的左侧,点B在原点的右侧),与y轴交于点C,OB=OC=3.
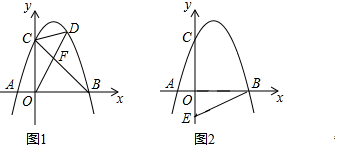
(1)求该抛物线的函数解析式;
(2)如图1,连接BC,点D是直线BC上方抛物线上的点,连接OD,CD,OD交BC于点F,当S△COF:S△CDF=3:2时,求点D的坐标.
(3)如图2,点E的坐标为(0,![]() ),在抛物线上是否存在点P,使∠OBP=2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.
),在抛物线上是否存在点P,使∠OBP=2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的不等式组![]() 的整数解个数不少于3个,但不多于5个,且关于y的分式方程
的整数解个数不少于3个,但不多于5个,且关于y的分式方程![]() 的解为整数,则符合条件的所有整数m的和为( )
的解为整数,则符合条件的所有整数m的和为( )
A.﹣24B.﹣19C.﹣16D.﹣10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x函数y=|﹣x2+bx﹣7|﹣4,点(4,5)在函数上,且b为整数,根据我们已有的研究函数的经验,请对该函数及其图象进行如下探究,并完成以下问题:
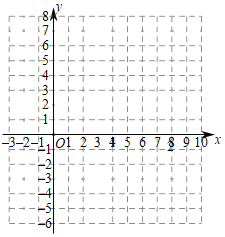
(1)求b= ;
(2)函数图象探究:
①下表是y与x的几组对应值,请直接写出m与n的值:m= ,n= ;
x | … | ﹣ | 0 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 7 | 8 | 8 | … |
y | … | m | 3 |
| ﹣4 | 1 | 4 | n | 4 | 1 | ﹣4 |
| 3 | 5 | … |
②根据你喜欢的方式,在如图所示的平面直角坐标系中,画出该函数图象;
(3)结果函数图象,写出该函数的一条性质: ;
(4)若关于x的方程|﹣x2+bx﹣7|=m+4有四个根,则m的取值范围为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明设计的“在一个平行四边形内作菱形”的尺规作图过程.
已知:四边形![]() 是平行四边形.
是平行四边形.
求作:菱形![]() (点
(点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上).
上).
作法:①以![]() 为圆心,
为圆心,![]() 长为半径作弧,交
长为半径作弧,交![]() 于点
于点![]() ;
;
②以![]() 为圆心,
为圆心,![]() 长为半径作弧,交
长为半径作弧,交![]() 于点
于点![]() ;
;
③连接![]() .所以四边形
.所以四边形![]() 为所求作的菱形.
为所求作的菱形.
根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵![]() ,
,![]() ,
,
∴ = .
在![]() 中,
中,![]() .
.
即![]() .
.
∴四边形![]() 为平行四边形.
为平行四边形.
∵![]() ,
,
∴四边形![]() 为菱形( )(填推理的依据).
为菱形( )(填推理的依据).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,关于x的一次函数y=k1x+b的图象与反比例函数y=![]() 的图象相交于A(﹣2,8),B(4,m)两点.
的图象相交于A(﹣2,8),B(4,m)两点.
(1)求一次函数与反比例函数的解析式.
(2)设一次函数y=k1x+b的图象与x轴,y轴的交点分别为M,N,P是x轴上一动点,当以P,M,N三点为顶点的三角形是等腰三角形时,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com