
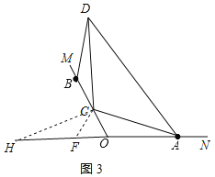
【题目】已知∠MON=120°,点A,B分别在ON,OM边上,且OA=OB,点C在线段OB上(不与点O,B重合),连接CA.将射线CA绕点C逆时针旋转120°得到射线CA′,将射线BO绕点B逆时针旋转150°与射线CA′交于点D.

(1)根据题意补全图1;
(2)求证:
①∠OAC=∠DCB;
②CD=CA(提示:可以在OA上截取OE=OC,连接CE);
(3)点H在线段AO的延长线上,当线段OH,OC,OA满足什么等量关系时,对于任意的点C都有∠DCH=2∠DAH,写出你的猜想并证明.
【答案】(1)见解析;(2)①见解析;②见解析;(3)猜想OH﹣OC=OA时,对于任意的点C都有∠DCH=2∠DAH;理由见解析
【解析】
(1)根据题意即可补全图形;
(2)①由旋转得∠ACD=120°,由三角形内角和得出∠DCB+∠ACO=60°,∠OAC+∠ACO=60°,即可得出结论;
②在OA上截取OE=OC,连接CE,则∠OEC=∠OCE=![]() (180°﹣∠MON)=30°,∠AEC=150°,得出∠AEC=∠CBD,易证AE=BC,由ASA证得△AEC≌△CBD,即可得出结论;
(180°﹣∠MON)=30°,∠AEC=150°,得出∠AEC=∠CBD,易证AE=BC,由ASA证得△AEC≌△CBD,即可得出结论;
(3)猜想OH﹣OC=OA时,对于任意的点C都有∠DCH=2∠DAH,在OH上截取OF=OC,连接CF、CH,则FH=OA,∠COF=180°﹣∠MON=60°,得出△OFC 是等边三角形,则CF=OC,∠CFH=∠COA=120°,由SAS证得△CFH≌△COA,得出∠H=∠OAC,由三角形外角性质得出∠BCH=∠COF+∠H=60°+∠H=60°+∠OAC,则∠DCH=60°+∠H+∠DCB=60°+2∠OAC,由CA=CD,∠ACD=120°,得出∠CAD=30°,即可得出∠DCH=2∠DAH.
解:(1)根据题意补全图形,如图1所示:
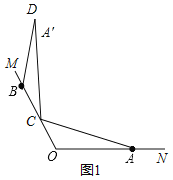
(2)证明:①由旋转得:∠ACD=120°,
∴∠DCB+∠ACO=180°﹣120°=60°,
∵∠MON=120°,
∴∠OAC+∠ACO=180°﹣120°=60°,
∴∠OAC=∠DCB;
②在OA上截取OE=OC,连接CE,如图2所示:
则∠OEC=∠OCE=![]() (180°﹣∠MON)=
(180°﹣∠MON)=![]() (180°﹣120°)=30°,
(180°﹣120°)=30°,
∴∠AEC=180°﹣∠OEC=180°﹣30°=150°,
由旋转得:∠CBD=150°,
∴∠AEC=∠CBD,
∵OA=OB,OE=OC,
∴AE=BC,在△AEC和△CBD中,
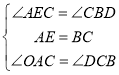 ,
,
∴△AEC≌△CBD(ASA),
∴CD=CA;
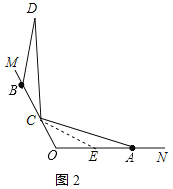
(3)解:猜想OH﹣OC=OA时,对于任意的点C都有∠DCH=2∠DAH;理由如下:
在OH上截取OF=OC,连接CF、CH,如图3所示:
则FH=OA,∠COF=180°﹣∠MON=180°﹣120°=60°,
∴△OFC 是等边三角形,
∴CF=OC,∠CFH=∠COA=120°,
在△CFH和△COA中,
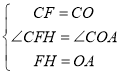 ,
,
∴△CFH≌△COA(SAS),
∴∠H=∠OAC,
∴∠BCH=∠COF+∠H=60°+∠H=60°+∠OAC,
∴∠DCH=60°+∠H+∠DCB=60°+2∠OAC,
∵CA=CD,∠ACD=120°,
∴∠CAD=30°,
∴∠DCH=2(∠CAD+∠OAC)=2∠DAH.


科目:初中数学 来源: 题型:
【题目】如图,已知△AOB与△A1OB1是以点O为位似中心的位似图形,且相似比为1:2,点B的坐标为(-1,2),则点B1的坐标为( )

A.(2,-4)B.(1,-4)C.(-1,4)D.(-4,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】1637年笛卡儿(R.Descartes,1596-1650)在其《几何学》中,首次应用待定系数法最早给出因式分解定理.关于笛卡尔的“待定系数法”原理,举例说明如下:
分解因式:![]() .观察知,显然
.观察知,显然![]() 时,原式
时,原式![]() ,因此原式可分解为
,因此原式可分解为![]() 与另一个整式的积.令:
与另一个整式的积.令:![]() ,而
,而![]() ,因等式两边
,因等式两边![]() 同次幂的系数相等,则有:
同次幂的系数相等,则有: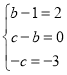 ,得
,得![]() ,从而
,从而![]()
根据以上材料,理解并运用材料提供的方法,解答以下问题:
(1)若![]() 是多项式
是多项式![]() 的因式,求
的因式,求![]() 的值并将多项式
的值并将多项式![]() 分解因式.
分解因式.
(2)若多项式![]() 含有因式
含有因式![]() 及
及![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产的一种商品其售价是成本的1.5倍,当售价降低5元时商品的利润率为25%.若不进行任何推广年销售量为1万件.为了获得更好的利益,公司准备拿出一定的资金做推广,根据经验,每年投入的推广费x万元时销售量y(万件)是x的二次函数:当x为1万元时,y是1.5(万件).当x为2万元时,y是1.8(万件).
(1)求该商品每件的的成本与售价分别是多少元?
(2)求出年利润与年推广费x的函数关系式;
(3)如果投入的年推广告费为1万到3万元(包括1万和3万元),问推广费在什么范同内,公司获得的年利润随推广费的增大而增大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了调查学生对垃圾分类及投放知识的了解情况,从甲、乙两校各随机抽取40名学生进行了相关知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.
a.甲、乙两校40名学生成绩的频数分布统计表如下:
成绩x 学校 |
|
|
|
|
|
甲 | 4 | 11 | 13 | 10 | 2 |
乙 | 6 | 3 | 15 | 14 | 2 |
(说明:成绩80分及以上为优秀,70~79分为良好,60~69分为合格,60分以下为不合格)
b.甲校成绩在![]() 这一组的是:
这一组的是:
70 70 70 71 72 73 73 73 74 75 76 77 78
c.甲、乙两校成绩的平均分、中位数、众数如下:
学校 | 平均分 | 中位数 | 众数 |
甲 | 74.2 | n | 5 |
乙 | 73.5 | 76 | 84 |
根据以上信息,回答下列问题:
(1)写出表中n的值;
(2)在此次测试中,某学生的成绩是74分,在他所属学校排在前20名,由表中数据可知该学生是_____________校的学生(填“甲”或“乙”),理由是__________;
(3)假设乙校800名学生都参加此次测试,估计成绩优秀的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
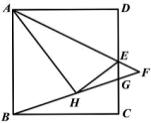
【题目】如图,在正方形ABCD中,AB=2,点E是CD的中点,连接AE,将△ADE沿AE折叠至△AHE,连接BH,延长AE,BH交于点F;BF,CD交于点G,则FG=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
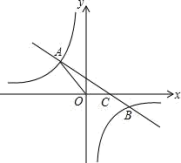
【题目】如图,一次函数y=kx+b(k≠0)的图象与反比例函数![]() 的图象交于二、四象限内的A、B两点,与x轴交于C点,点A的坐标为(﹣2,3),点B的坐标为(4,n).
的图象交于二、四象限内的A、B两点,与x轴交于C点,点A的坐标为(﹣2,3),点B的坐标为(4,n).
(1)求该反比例函数和一次函数的解析式;
(2)在x轴上是否存在点P,使△APC是直角三角形?若存,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把![]() 个只有颜色不同的小球分别装入甲乙丙三个布袋里其中甲布袋里有
个只有颜色不同的小球分别装入甲乙丙三个布袋里其中甲布袋里有![]() 个红球,
个红球,![]() 个白球;乙布袋里有
个白球;乙布袋里有![]() 个红球,
个红球,![]() 个白球;丙布袋里有
个白球;丙布袋里有![]() 个红球,
个红球,![]() 个白球.
个白球.
![]() 求
求![]() 的值,并求从甲、乙两个布袋中随机各摸出
的值,并求从甲、乙两个布袋中随机各摸出![]() 个小球,求摸出的两个小球都是红球的概率;
个小球,求摸出的两个小球都是红球的概率;
![]() 利用列表或树状图法求从甲、乙、丙三个布袋中随机各摸出
利用列表或树状图法求从甲、乙、丙三个布袋中随机各摸出![]() 个小球,求摸出的三个小球是一红二白的概率.
个小球,求摸出的三个小球是一红二白的概率.
![]() 将丙袋子中原有的所有小球拿出,另装
将丙袋子中原有的所有小球拿出,另装![]() 个只有颜色不同的球,其中
个只有颜色不同的球,其中![]() 个白球,
个白球,![]() 个红球,若从袋中取出若千个红球,换成相同数量的黄球.搅拌均匀后,使得随机从袋中摸出两个球,颜色是一白一黄的概率为
个红球,若从袋中取出若千个红球,换成相同数量的黄球.搅拌均匀后,使得随机从袋中摸出两个球,颜色是一白一黄的概率为![]() ,(不放回拿球)求袋中有几个红球被换成了黄球?
,(不放回拿球)求袋中有几个红球被换成了黄球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为半圆O的直径,点C在半圆上,过点O作BC的平行线交AC于点E,交过点A的直线于点D,且∠D=∠BAC
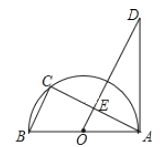
(1)求证:AD是半圆O的切线;
(2)求证:△ABC∽△DOA;
(3)若BC=2,CE=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com