
【题目】1637年笛卡儿(R.Descartes,1596-1650)在其《几何学》中,首次应用待定系数法最早给出因式分解定理.关于笛卡尔的“待定系数法”原理,举例说明如下:
分解因式:![]() .观察知,显然
.观察知,显然![]() 时,原式
时,原式![]() ,因此原式可分解为
,因此原式可分解为![]() 与另一个整式的积.令:
与另一个整式的积.令:![]() ,而
,而![]() ,因等式两边
,因等式两边![]() 同次幂的系数相等,则有:
同次幂的系数相等,则有: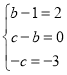 ,得
,得![]() ,从而
,从而![]()
根据以上材料,理解并运用材料提供的方法,解答以下问题:
(1)若![]() 是多项式
是多项式![]() 的因式,求
的因式,求![]() 的值并将多项式
的值并将多项式![]() 分解因式.
分解因式.
(2)若多项式![]() 含有因式
含有因式![]() 及
及![]() ,求
,求![]() 的值.
的值.
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AD⊥BC 于 D(其中 BD>CD),BE⊥AC 于 E,AD 与 BE 相交于点 F,直线 AD 与△BCF 的外接圆 O 交于点 H,点 M 在圆 O 上,满足弧 HM=弧 CF,连接 FM.
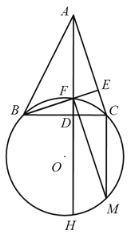
(1)求证:AF=CM;
(2)若∠ABE=45°,FH ![]() ,圆O的直径为
,圆O的直径为![]() ,求BF的值.
,求BF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
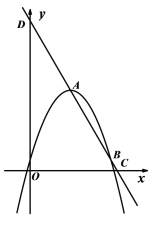
【题目】如图所示,二次函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于A、B两点,点B在点A的右侧,直线AB分别交x轴、y轴于C、D两点,且k<0.
的图象交于A、B两点,点B在点A的右侧,直线AB分别交x轴、y轴于C、D两点,且k<0.
(1)求A,B两点横坐标;
(2)若△OAB是以OA为腰的等腰三角形,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了创建文明城市,增弘环保意识,某班随机抽取了8名学生(分别为A,B,C,D,E,F,G,H),进行垃圾分类投放检测,检测结果如下表,其中“√”表示投放正确,“×”表示投放错误,
学生 垃圾类别 | A | B | C | D | E | F | G | H |
可回收物 | √ | × | × | √ | √ | × | √ | √ |
其他垃圾 | × | √ | √ | √ | √ | × | √ | √ |
餐厨垃圾 | √ | √ | √ | √ | √ | √ | √ | √ |
有害垃圾 | × | √ | × | × | × | √ | × | √ |
(1)检测结果中,有几名学生正确投放了至少三类垃圾?请列举出这几名学生.
(2)为进一步了解学生垃圾分类的投放情况,从检测结果是“有害垃圾”投放错误的学生中随机抽取2名进行访谈,求抽到学生A的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
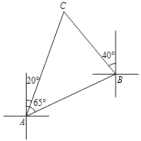
【题目】如图,一艘船由![]() 港沿北偏东65°方向航行
港沿北偏东65°方向航行![]() 至
至![]() 港,然后再沿北偏西40°方向航行至
港,然后再沿北偏西40°方向航行至![]() 港,
港,![]() 港在
港在![]() 港北偏东20°方向,则
港北偏东20°方向,则![]() 两港之间的距离为( )
两港之间的距离为( )![]() .
.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了丰富学生课余生活,开展了“第二课堂”活动,推出了以下四种选修课程:![]() .绘画;
.绘画;![]() .唱歌;
.唱歌;![]() .跳舞;
.跳舞;![]() .演讲;
.演讲;![]() .书法.学校规定:每个学生都必须报名且只能选择其中的一个课程.学校随机抽查了部分学生,对他们选择的课程情况进行了统计,并绘制了如下两幅不完整的统计图.
.书法.学校规定:每个学生都必须报名且只能选择其中的一个课程.学校随机抽查了部分学生,对他们选择的课程情况进行了统计,并绘制了如下两幅不完整的统计图.
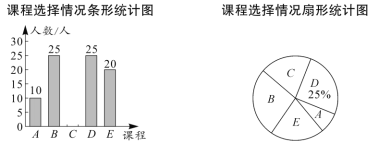
请结合统计图中的信息解决下列问题:
(1)这次抽查的学生人数是多少人?
(2)将条形统计图补充完整.
(3)求扇形统计图中课程![]() 所对应扇形的圆心角的度数.
所对应扇形的圆心角的度数.
(4)如果该校共有1200名学生,请你估计该校选择课程![]() 的学生约有多少人.
的学生约有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD中,AD∥BC,AB=BC=4,∠B=60°,∠C=105°,点E为BC的中点,以CE为弦作圆,设该圆与四边形ABCD的一边的交点为P,若∠CPE=30°,则EP的长为_____.
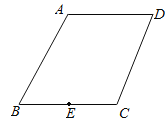
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠MON=120°,点A,B分别在ON,OM边上,且OA=OB,点C在线段OB上(不与点O,B重合),连接CA.将射线CA绕点C逆时针旋转120°得到射线CA′,将射线BO绕点B逆时针旋转150°与射线CA′交于点D.

(1)根据题意补全图1;
(2)求证:
①∠OAC=∠DCB;
②CD=CA(提示:可以在OA上截取OE=OC,连接CE);
(3)点H在线段AO的延长线上,当线段OH,OC,OA满足什么等量关系时,对于任意的点C都有∠DCH=2∠DAH,写出你的猜想并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业为响应国家教育扶贫的号召,决定对某乡镇全体贫困初、高中学生进行资助,初中学生每月资助200元,高中学生每月资助300元.已知该乡受资助的初中学生人数是受资助的高中学生人数的2倍,且该企业在2018年下半年7﹣12月这6个月资助学生共支出10.5万元.
(1)问该乡镇分别有多少名初中学生和高中学生获得了资助?
(2)2018年7﹣12月期间,受资助的初、高中学生中,分别有30%和40%的学生被评为优秀学生,从而获得了该乡镇政府的公开表扬.同时,提供资助的企业为了激发更多受资助学生的进取心和学习热情,决定对2019年上半年1﹣6月被评为优秀学生的初中学生每人每月增加a%的资助,对被评为优秀学生的高中学生每人每月增加2a%的资助.在此奖励政策的鼓励下,2019年1﹣6月被评为优秀学生的初、高中学生分別比2018年7﹣12月的人数增加了3a%、a%.这样,2019年上半年评为优秀学生的初、高中学生所获得的资助总金额一个月就达到了10800元,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com