练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

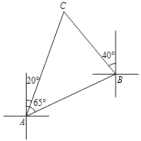
    【题目】如图，一艘船由港沿北偏东65°方向航行至港，然后再沿北偏西40°方向航行至港，港在港北偏东20°方向，则两港之间的距离为（　　）．

    A.B.C.D.

    【答案】B

    【解析】

    根据题意得，∠CAB=65°-20°，∠ACB=40°+20°=60°，AB=30，过B作BE⊥AC于E，解直角三角形即可得到结论．

    解：根据题意得，∠CAB=65°-20°=45°，∠ACB=40°+20°=60°，AB=30，

    过B作BE⊥AC于E，


    ∴∠AEB=∠CEB=90°，
    在Rt△ABE中，∵∠ABE=45°，AB=30，
    ∴AE=BE=AB=30km，
    在Rt△CBE中，∵∠ACB=60°，
    ∴CE=BE=10km，
    ∴AC=AE+CE=30+10，
    ∴A，C两港之间的距离为（30+10）km，
    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，AB是⊙O的直径，AC是弦，CD是⊙O的切线，C为切点，AD⊥CD于点D．

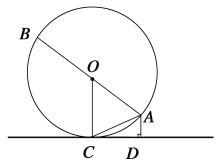
    求证：（1）∠AOC=2∠ACD；（2）AC2＝AB·AD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

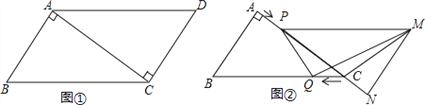
    【题目】已知，如图①，在ABCD中，AB=3cm，BC=5cm，AC⊥AB，△ACD沿AC的方向匀速平移得到△PNM，速度为1cm/s；同时，点Q从点C出发，沿CB方向匀速移动，速度为1cm/s，当△PNM停止平移时，点Q也停止移动，如图②，设移动时间为t（s）（0＜t＜4），连接PQ，MQ，MC，解答下列问题：

    （1）当t为何值时，PQ∥MN？

    （2）设△QMC的面积为y（cm2），求y与t之间的函数关系式；

    （3）是否存在某一时刻t，使S△QMC：S四边形ABQP=1：4？若存在，求出t的值；若不存在，请说明理由．

    （4）是否存在某一时刻t，使PQ⊥MQ？若存在，求出t的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

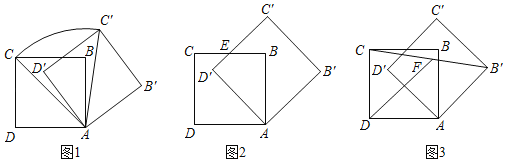
    【题目】若边长为6的正方形ABCD绕点A顺时针旋转，得正方形AB′C′D′，记旋转角为a．

    （I）如图1，当a＝60°时，求点C经过的弧的长度和线段AC扫过的扇形面积；

    （Ⅱ）如图2，当a＝45°时，BC与D′C′的交点为E，求线段D′E的长度；

    （Ⅲ）如图3，在旋转过程中，若F为线段CB′的中点，求线段DF长度的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为改善生态环境，建设美丽乡村，某村规划将一块长18米，宽10米的矩形场地建设成绿化广场，如图，内部修建三条宽相等的小路，其中一条路与广场的长平行，另两条路与广场的宽平行，其余区域种植绿化，使绿化区域的面积为广场总面积的80%．

    （1）求该广场绿化区域的面积；

    （2）求广场中间小路的宽．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】1637年笛卡儿（R．Descartes，1596-1650）在其《几何学》中，首次应用待定系数法最早给出因式分解定理．关于笛卡尔的“待定系数法”原理，举例说明如下：

    分解因式：．观察知，显然时，原式，因此原式可分解为与另一个整式的积．令：，而，因等式两边同次幂的系数相等，则有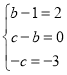：，得，从而

    根据以上材料，理解并运用材料提供的方法，解答以下问题：

    （1）若是多项式的因式，求的值并将多项式分解因式．

    （2）若多项式含有因式及，求的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一次函数的图像与反比例函数的图像交于，两点，与轴分别交于两点，且．

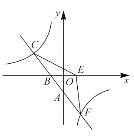
    （1）求一次函数和反比例函数的解析式；

    （2）若点与点关于轴对称，连接，求的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了调查学生对垃圾分类及投放知识的了解情况，从甲、乙两校各随机抽取40名学生进行了相关知识测试，获得了他们的成绩（百分制），并对数据（成绩）进行了整理、描述和分析．下面给出了部分信息．

    a．甲、乙两校40名学生成绩的频数分布统计表如下：

    成绩x

    学校

    甲

    4

    11

    13

    10

    2

    乙

    6

    3

    15

    14

    2

    （说明：成绩80分及以上为优秀，70~79分为良好，60~69分为合格，60分以下为不合格）

    b．甲校成绩在这一组的是：

    70 70 70 71 72 73 73 73 74 75 76 77 78

    c．甲、乙两校成绩的平均分、中位数、众数如下：

    学校

    平均分

    中位数

    众数

    甲

    74.2

    n

    5

    乙

    73.5

    76

    84

    根据以上信息，回答下列问题：

    （1）写出表中n的值；

    （2）在此次测试中，某学生的成绩是74分，在他所属学校排在前20名，由表中数据可知该学生是_____________校的学生（填“甲”或“乙”），理由是__________；

    （3）假设乙校800名学生都参加此次测试，估计成绩优秀的学生人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】A，C，B三地依次在一条笔直的道路上甲、乙两车同时分别从A，B两地出发，相向而行．甲车从A地行驶到B地就停止，乙车从B地行驶到A地后，立即以相同的速度返回B地，在整个行驶的过程中，甲、乙两车均保持匀速行驶，甲、乙两车距C地的距离之和y（km）与甲车出发的间（b）之间的函数关系如图所示，则甲车到达B地时，乙车距B地的距离为_____km．

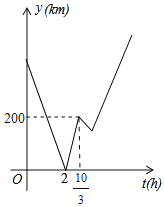
    查看答案和解析>>

    同步练习册答案