
【题目】如图,AB是⊙O的直径,AC是弦,CD是⊙O的切线,C为切点,AD⊥CD于点D.
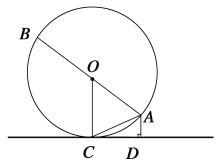
求证:(1)∠AOC=2∠ACD;(2)AC2=AB·AD.
【答案】(1)证明见解析;(2)证明见解析
【解析】
试题分析:(1)根据CD为切线得出∠ACD+∠ACO=90°,根据OC=OA得出∠ACO=∠CAO,即![]() ∠AOC+∠ACO=90°,将两式联立得出答案;(2)连接BC,根据AB为直径得出∠ACB=90°,结合∠AOC=2∠B得出∠B=∠ACD,从而得到△ACD∽△ABC,得出答案.
∠AOC+∠ACO=90°,将两式联立得出答案;(2)连接BC,根据AB为直径得出∠ACB=90°,结合∠AOC=2∠B得出∠B=∠ACD,从而得到△ACD∽△ABC,得出答案.
试题解析:(1)∵CD是⊙O的切线,∴∠OCD=90°, 即∠ACD+∠ACO=90°.…①
∵OC=OA,∴∠ACO=∠CAO, ∴∠AOC=180°-2∠ACO,即![]() ∠AOC+∠ACO=90°.…②
∠AOC+∠ACO=90°.…②
由①,②,得:∠ACD-![]() ∠AOC=0,即∠AOC=2∠ACD;
∠AOC=0,即∠AOC=2∠ACD;
(2)如图,连接BC.
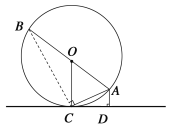
∵AB是直径,∴∠ACB=90° 在Rt△ACD与△RtABC中,∵∠AOC=2∠B,
∴∠B=∠ACD, ∴△ACD∽△ABC, ∴![]() =AB·AD
=AB·AD


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
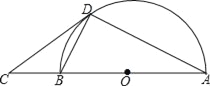
【题目】如图,AB是半圆O的直径,C是AB延长线上一点,CD与半圆O相切于点D,连接AD,BD.
(1)求证:∠BAD=∠BDC;
(2)若sin∠BDC=![]() ,BC=2,求⊙O的半径.
,BC=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
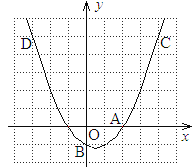
【题目】如图,已知二次函数![]() 的图象过A(2,0),B(0,-1)和C(4,5)三点。
的图象过A(2,0),B(0,-1)和C(4,5)三点。
(1)求二次函数的解析式;
(2)设二次函数的图象与![]() 轴的另一个交点为D,求点D的坐标;
轴的另一个交点为D,求点D的坐标;
(3)在同一坐标系中画出直线![]() ,并写出当
,并写出当![]() 在什么范围内时,一次函数的值大于二次函数的值。
在什么范围内时,一次函数的值大于二次函数的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于钝角α,定义它的三角函数值如下:sinα=sin (180°-α),cosα=-cos (180°-α);若一个三角形的三个内角的比是1∶1∶4,A,B是这个三角形的两个顶点,sinA,cosB是方程4x2-mx-1=0的两个不相等的实数根,求m的值及∠A和∠B的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法不正确的是( )
A. 以等腰三角形顶角的顶点为圆心,底边上的高为半径的圆与底边相切
B. 若两个三角形的边长为8、6、4和4![]() 、3
、3![]() 、2
、2![]() ,则这两个三角形相似
,则这两个三角形相似
C. 梯形的中位线平行于两底,并且等于两底和的一半
D. 命题“两圆外离,则两圆无公共点”的逆命题是真命题
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的半径为2,弦BC的长为![]() ,点A为弦BC所对优弧上任意一点(B,C两点除外).
,点A为弦BC所对优弧上任意一点(B,C两点除外).
 (1)求∠BAC的度数;
(1)求∠BAC的度数;
(2)求△ABC面积的最大值.
(参考数据:![]() ,
,![]() ,
,![]() .)
.)
查看答案和解析>>
科目:初中数学 来源: 题型:
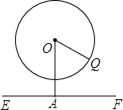
【题目】“五一”节,小雯和同学一起到游乐场玩大型摩天轮,摩天轮的半径为20m,匀速转动一周需要12min,小雯所坐最底部的车厢(离地面0.5m).
(1)经过2min后小雯到达点Q,如图所示,此时他离地面的高度是多少?
(2)在摩天轮滚动的过程中,小雯将有多长时间连续保持在离地面不低于30.5m的空中?
查看答案和解析>>
科目:初中数学 来源: 题型:
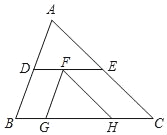
【题目】如图,在△ABC中,D、E分别是边AB、AC上的点,DE∥BC,点F在线段DE上,过点F作FG∥AB、FH∥AC分别交BC于点G、H,如果BG:GH:HC=2:4:3.求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线l和l外一点C.
求作:经过点C且垂直于l的直线.
作法:如图,
(1)在直线l上任取点A;
(2)以点C为圆心,AC为半径作圆,交直线l于点B;
(3)分别以点A,B为圆心,大于![]() 的长为半径作弧,两弧相交于点D;
的长为半径作弧,两弧相交于点D;
(4)作直线CD.
所以直线CD就是所求作的垂线.
(1)请使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:连接AC,BC,AD,BD.
∵AC=BC, = ,
∴CD⊥AB(依据: ).
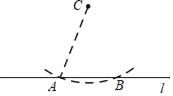
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com