
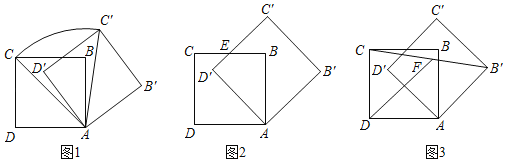
【题目】若边长为6的正方形ABCD绕点A顺时针旋转,得正方形AB′C′D′,记旋转角为a.
(I)如图1,当a=60°时,求点C经过的弧![]() 的长度和线段AC扫过的扇形面积;
的长度和线段AC扫过的扇形面积;
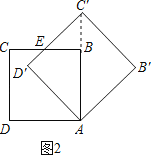
(Ⅱ)如图2,当a=45°时,BC与D′C′的交点为E,求线段D′E的长度;
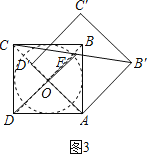
(Ⅲ)如图3,在旋转过程中,若F为线段CB′的中点,求线段DF长度的取值范围.
【答案】(I)12π;(Ⅱ)D′E=6![]() ﹣6;(Ⅲ)3
﹣6;(Ⅲ)3![]() ﹣3≤DF≤3
﹣3≤DF≤3![]() +3.
+3.
【解析】
(Ⅰ)根据正方形的性质得到AD=CD=6,∠D=90°,由勾股定理得到AC=6![]() ,根据弧长的计算公式和扇形的面积公式即可得到结论;
,根据弧长的计算公式和扇形的面积公式即可得到结论;
(Ⅱ)连接BC′,根据题意得到B在对角线AC′上,根据勾股定理得到AC′=![]() =6
=6![]() ,求得BC′=6
,求得BC′=6![]() ﹣6,推出△BC′E是等腰直角三角形,得到C′E=
﹣6,推出△BC′E是等腰直角三角形,得到C′E=![]() BC′=12﹣6
BC′=12﹣6![]() ,于是得到结论;
,于是得到结论;
(Ⅲ)如图3,连接DB,AC相交于点O,则O是DB的中点,根据三角形中位线定理得到FO=![]() AB′=3,推出F在以O为圆心,3为半径的圆上运动,于是得到结论.
AB′=3,推出F在以O为圆心,3为半径的圆上运动,于是得到结论.
解:(Ⅰ)∵四边形ABCD是正方形,
∴AD=CD=6,∠D=90°,
∴AC=6![]() ,
,
∵边长为6的正方形ABCD绕点A顺时针旋转,得正方形AB′C′D′,
∴∠CAC′=60°,
∴![]() 的长度=
的长度=![]() =2
=2![]() π,线段AC扫过的扇形面积=
π,线段AC扫过的扇形面积=![]() =12π;
=12π;
(Ⅱ)解:如图2,连接BC′,
∵旋转角∠BAB′=45°,∠BAD′=45°,
∴B在对角线AC′上,
∵B′C′=AB′=6,
在Rt△AB′C′中,AC′=![]() =6
=6![]() ,
,
∴BC′=6![]() ﹣6,
﹣6,
∵∠C′BE=180°﹣∠ABC=90°,∠BC′E=90°﹣45°=45°,
∴△BC′E是等腰直角三角形,
∴C′E=![]() BC′=12﹣6
BC′=12﹣6![]() ,
,
∴D′E=C′D′﹣EC′=6﹣(12﹣6![]() )=6
)=6![]() ﹣6;
﹣6;
(Ⅲ)如图3,连接DB,AC相交于点O,
则O是DB的中点,
∵F为线段BC′的中点,
∴FO=![]() AB′=3,
AB′=3,
∴F在以O为圆心,3为半径的圆上运动,
∵DO=3![]() ,
,
∴DF最大值为3![]() +3,DF的最小值为3
+3,DF的最小值为3![]() ﹣3,
﹣3,
∴DF长的取值范围为3![]() ﹣3≤DF≤3
﹣3≤DF≤3![]() +3.
+3.


科目:初中数学 来源: 题型:
【题目】如图,已知线段![]() ,点
,点![]() 为线段外一点,且
为线段外一点,且![]() .
.
(1)请用直尺(不带刻度)和圆规在线段![]() 上找一点
上找一点![]() ,使得
,使得![]() 的周长为
的周长为![]() (作图不必写作法,但要保留作图痕迹);
(作图不必写作法,但要保留作图痕迹);
(2)在(1)的条件下,若![]() ,
,![]() ,当
,当![]() 是等腰三角形时,求
是等腰三角形时,求![]() 的面积.
的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足社区居民健身的需要,区政府准备采购若干套健身器材免费提供给社区,经考察,康乐公司有甲,乙两种型号的健身器材可供选择.
(1)康乐公司2017年每套甲型健身器材的售价为2万元,经过连续两年降价,2019年每套售价为1.28万元,求每套甲型健身器材售价的年平均下降率n;
(2)2019年市政府经过招标,决定年内采购并安装康乐公司甲,乙两种型号的健身器材共80套,采购专项经费总计不超过95万元,采购合同规定:每套甲型健身器材售价为1.28万元,每套乙型健身器材售价为1.4(1﹣n)万元.
①甲型健身器材最多可购买多少套?
②按照甲型健身器材购买最多的情况下,安装完成后,若每套甲型和乙型健身器材一年的养护费分别是购买价的8%和10%,区政府计划支出9万元进行养护,问该计划支出能否满足一年的养护需要?
查看答案和解析>>
科目:初中数学 来源: 题型:
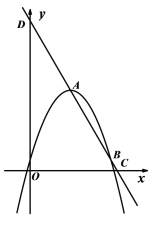
【题目】如图所示,二次函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于A、B两点,点B在点A的右侧,直线AB分别交x轴、y轴于C、D两点,且k<0.
的图象交于A、B两点,点B在点A的右侧,直线AB分别交x轴、y轴于C、D两点,且k<0.
(1)求A,B两点横坐标;
(2)若△OAB是以OA为腰的等腰三角形,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边AD⊥y轴,垂足为点E,顶点A在第二象限,顶点B在y轴的正半轴上,反比例函数y=![]() (k≠0,x>0)的图象经过顶点C、D,若点C的横坐标为5,BE=3DE,则k的值为______.
(k≠0,x>0)的图象经过顶点C、D,若点C的横坐标为5,BE=3DE,则k的值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了创建文明城市,增弘环保意识,某班随机抽取了8名学生(分别为A,B,C,D,E,F,G,H),进行垃圾分类投放检测,检测结果如下表,其中“√”表示投放正确,“×”表示投放错误,
学生 垃圾类别 | A | B | C | D | E | F | G | H |
可回收物 | √ | × | × | √ | √ | × | √ | √ |
其他垃圾 | × | √ | √ | √ | √ | × | √ | √ |
餐厨垃圾 | √ | √ | √ | √ | √ | √ | √ | √ |
有害垃圾 | × | √ | × | × | × | √ | × | √ |
(1)检测结果中,有几名学生正确投放了至少三类垃圾?请列举出这几名学生.
(2)为进一步了解学生垃圾分类的投放情况,从检测结果是“有害垃圾”投放错误的学生中随机抽取2名进行访谈,求抽到学生A的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘船由![]() 港沿北偏东65°方向航行
港沿北偏东65°方向航行![]() 至
至![]() 港,然后再沿北偏西40°方向航行至
港,然后再沿北偏西40°方向航行至![]() 港,
港,![]() 港在
港在![]() 港北偏东20°方向,则
港北偏东20°方向,则![]() 两港之间的距离为( )
两港之间的距离为( )![]() .
.
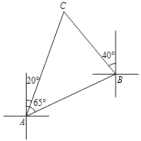
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
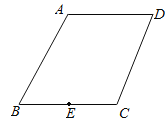
【题目】已知:如图,四边形ABCD中,AD∥BC,AB=BC=4,∠B=60°,∠C=105°,点E为BC的中点,以CE为弦作圆,设该圆与四边形ABCD的一边的交点为P,若∠CPE=30°,则EP的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com