
����Ŀ��Ϊ������������������Ҫ�����������ɹ�����������������ṩ�������������죬���ֹ�˾�мף��������ͺŵĽ������Ŀɹ�ѡ��
��1�����ֹ�˾2017��ÿ���ͽ������ĵ��ۼ�Ϊ2��Ԫ�������������꽵�ۣ�2019��ÿ���ۼ�Ϊ1.28��Ԫ����ÿ���ͽ��������ۼ۵���ƽ���½���n��
��2��2019�������������б꣬�������ڲɹ�����װ���ֹ�˾�ף��������ͺŵĽ������Ĺ�80�ף��ɹ�ר����ܼƲ�����95��Ԫ���ɹ���ͬ�涨��ÿ���ͽ��������ۼ�Ϊ1.28��Ԫ��ÿ�����ͽ��������ۼ�Ϊ1.4��1��n����Ԫ��
�����ͽ����������ɹ�������ף�
�����ռ��ͽ������Ĺ�����������£���װ��ɺ���ÿ���ͺ����ͽ�������һ��������ѷֱ��ǹ���۵�8%��10%���������ƻ�֧��9��Ԫ�����������ʸüƻ�֧���ܷ�����һ���������Ҫ��
���𰸡���1��ÿ���ͽ��������ۼ۵���ƽ���½���Ϊ0.2����2���ټ��ͽ����������ɹ���33�ף��ڸüƻ�֧��������һ���������Ҫ��
��������
��1������ԭ�ۼ��������ν��ۺ�ļ۸��ɵó�����n��һԪ���η��̣���֮ȡ����ֵ������⣻
��2�����蹺����ͽ�������x�ף��������ͽ������ģ�80��x���ף������ܼۣ�������������ϲɹ�ר����ܼƲ�����95��Ԫ�����ɵó�����x��һԪһ�β���ʽ����֮ȡ���е��������ֵ������⣻
�ڸ����ܼۣ��������������ÿ���ͺ����ͽ�������һ��������ѷֱ��ǹ���۵�8%��10%�������һ����Ҫ֧���������ѣ�������9��Ԫ���бȽϺ���⣮
�⣺��1�������⣬�ã�2��1��n��2��1.28��
��ã�n1��0.2��n2��1.8���������⣬��ȥ����
��ÿ���ͽ��������ۼ۵���ƽ���½���Ϊ0.2��
��2�����蹺����ͽ�������x�ף��������ͽ������ģ�80��x���ף�
�����⣬�ã�1.28x+1.4����1��0.2����80��x����95��
��ã�x��33![]() ��
��
��x��������
��x�����ֵΪ33��
�𣺼��ͽ����������ɹ���33�ף�
��1.28��33��8%+1.4����1��0.2������80��33����10%��8.6432����Ԫ����
��8.6432��9��
��üƻ�֧��������һ���������Ҫ��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˸��õ�����������ˮ�ʣ����������������۹�˾�������� 10 ̨��ˮ�����豸������ A��B �����ͺŵ��豸������ÿ̨�ļ۸��´�����ˮ�����±���
A �� | B �� | |
�۸���Ԫ/̨�� | a | b |
������ˮ�����֣��£� | 240 | 200 |
�����飺����һ̨ A ���豸�ȹ���һ̨ B ���豸�� 2 ��Ԫ������ 2 ̨ A ���豸�ȹ��� 3 ̨ B ���豸�� 6 ��Ԫ��
��1���� a��b ��ֵ��
��2����Ԥ�㣺�����۹�˾������ˮ�����豸���ʽ��� 105 ��Ԫ������Ϊ�ù�˾ ���ļ��ֹ�����
��3���ڣ�2���ʵ������£���ÿ��Ҫ��������������ˮ�������� 2040 �֣�Ϊ�˽� Լ�ʽ�����Ϊ���۹�˾���һ����ʡǮ�Ĺ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB����O��ֱ����AC���ң�CD����O�����ߣ�CΪ�е㣬AD��CD�ڵ�D��
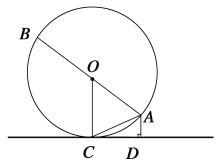
��֤����1����AOC=2��ACD����2��AC2��AB��AD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() �ϣ���
�ϣ���![]() ��ֱ��
��ֱ��![]() ��
��![]() ��
��![]() ����
����![]() �ӳ�����
�ӳ�����![]() ������
������![]() ��
��![]() ��
��![]() ����
����![]() �ij�Ϊ__________��
�ij�Ϊ__________��
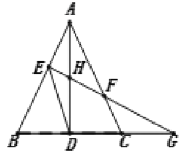
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���ֳ����Ƴ���һ�������ٷɳ�������Ŀ����Ŀ������б�¹�������㲻ͬ���Ѷ������οͿ��Գ�����ֱ��������AB��������ѡ����Ŀ�Ѷȣ�����б�¹��BC���¶ȣ����±ȣ�Ϊi��1��2��BC��12![]() �ף�CD��8�ף���D��36���������е�A��B��C��D����ͬһƽ���ڣ���ֱ��������AB�ĸ߶�ԼΪ���������ף�����ȷ��0.1�ף��ο����ݣ�tan36���0.73��cos36���0.81��sin36���0.59��
�ף�CD��8�ף���D��36���������е�A��B��C��D����ͬһƽ���ڣ���ֱ��������AB�ĸ߶�ԼΪ���������ף�����ȷ��0.1�ף��ο����ݣ�tan36���0.73��cos36���0.81��sin36���0.59��
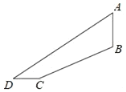
A.5.6B.6.9C.11.4D.13.9
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��AOB���A1OB1���Ե�OΪλ�����ĵ�λ��ͼ�Σ������Ʊ�Ϊ1��2����B������Ϊ��-1��2�������B1������Ϊ�� ��

A.��2��-4��B.��1��-4��C.��-1��4��D.��-4��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
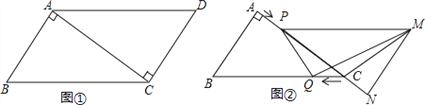
����Ŀ����֪����ͼ�٣���ABCD�У�AB=3cm��BC=5cm��AC��AB����ACD��AC�ķ�������ƽ�Ƶõ���PNM���ٶ�Ϊ1cm/s��ͬʱ����Q�ӵ�C��������CB���������ƶ����ٶ�Ϊ1cm/s������PNMֹͣƽ��ʱ����QҲֹͣ�ƶ�����ͼ�ڣ����ƶ�ʱ��Ϊt��s����0��t��4��������PQ��MQ��MC������������⣺
��1����tΪ��ֵʱ��PQ��MN��
��2�����QMC�����Ϊy��cm2������y��t֮��ĺ�����ϵʽ��
��3���Ƿ����ijһʱ��t��ʹS��QMC��S�ı���ABQP=1��4�������ڣ����t��ֵ���������ڣ���˵�����ɣ�
��4���Ƿ����ijһʱ��t��ʹPQ��MQ�������ڣ����t��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����߳�Ϊ6��������ABCD�Ƶ�A˳ʱ����ת����������AB��C��D�䣬����ת��Ϊa��
��I����ͼ1����a��60��ʱ�����C�����Ļ�![]() �ij��Ⱥ��߶�ACɨ�������������
�ij��Ⱥ��߶�ACɨ�������������
������ͼ2����a��45��ʱ��BC��D��C��Ľ���ΪE�����߶�D��E�ij��ȣ�
������ͼ3������ת�����У���FΪ�߶�CB����е㣬���߶�DF���ȵ�ȡֵ��Χ��
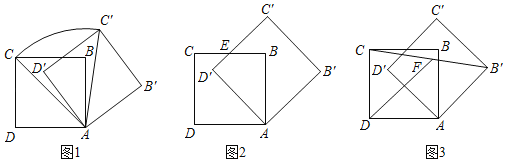
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˵���ѧ�����������༰Ͷ��֪ʶ���˽�������Ӽס�����У�������ȡ40��ѧ�����������֪ʶ���ԣ���������ǵijɼ����ٷ��ƣ����������ݣ��ɼ��������������������ͷ�������������˲�����Ϣ��
a���ס�����У40��ѧ���ɼ���Ƶ���ֲ�ͳ�Ʊ����£�
�ɼ�x ѧУ |
|
|
|
|
|
�� | 4 | 11 | 13 | 10 | 2 |
�� | 6 | 3 | 15 | 14 | 2 |
��˵�����ɼ�80�ּ�����Ϊ���㣬70~79��Ϊ���ã�60~69��Ϊ�ϸ�60������Ϊ���ϸ�
b����У�ɼ���![]() ��һ����ǣ�
��һ����ǣ�
70 70 70 71 72 73 73 73 74 75 76 77 78
c���ס�����У�ɼ���ƽ���֡���λ�����������£�
ѧУ | ƽ���� | ��λ�� | ���� |
�� | 74.2 | n | 5 |
�� | 73.5 | 76 | 84 |
����������Ϣ���ش��������⣺
��1��д������n��ֵ��
��2���ڴ˴β����У�ijѧ���ijɼ���74�֣���������ѧУ����ǰ20�����ɱ������ݿ�֪��ѧ����_____________У��ѧ������������������������������__________��
��3��������У800��ѧ�����μӴ˴β��ԣ����Ƴɼ������ѧ��������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com