
【题目】如图,已知△AOB与△A1OB1是以点O为位似中心的位似图形,且相似比为1:2,点B的坐标为(-1,2),则点B1的坐标为( )

A.(2,-4)B.(1,-4)C.(-1,4)D.(-4,2)
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AD⊥BC 于 D(其中 BD>CD),BE⊥AC 于 E,AD 与 BE 相交于点 F,直线 AD 与△BCF 的外接圆 O 交于点 H,点 M 在圆 O 上,满足弧 HM=弧 CF,连接 FM.
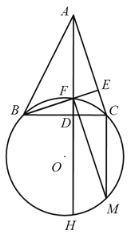
(1)求证:AF=CM;
(2)若∠ABE=45°,FH ![]() ,圆O的直径为
,圆O的直径为![]() ,求BF的值.
,求BF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解中考体育科目训练情况,某区从全区九年级学生中随机抽取了部分学生进行了一次中考体育科目测试(把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格:D级:不及格),并将测试结果绘成了如下两幅不完整的统计图。请根据统计图中的信息解答下列问题:
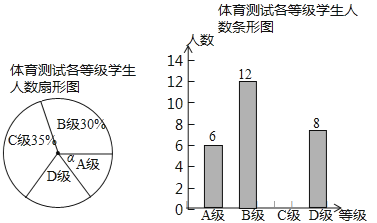
(1)求本次抽样测试的学生人数是多少?
(2)通过计算把图中的条形统计图补充完整
(3)该区九年级有学生7000名,如果全部参加这次中考体育科目测试请估计不及格人数有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足社区居民健身的需要,区政府准备采购若干套健身器材免费提供给社区,经考察,康乐公司有甲,乙两种型号的健身器材可供选择.
(1)康乐公司2017年每套甲型健身器材的售价为2万元,经过连续两年降价,2019年每套售价为1.28万元,求每套甲型健身器材售价的年平均下降率n;
(2)2019年市政府经过招标,决定年内采购并安装康乐公司甲,乙两种型号的健身器材共80套,采购专项经费总计不超过95万元,采购合同规定:每套甲型健身器材售价为1.28万元,每套乙型健身器材售价为1.4(1﹣n)万元.
①甲型健身器材最多可购买多少套?
②按照甲型健身器材购买最多的情况下,安装完成后,若每套甲型和乙型健身器材一年的养护费分别是购买价的8%和10%,区政府计划支出9万元进行养护,问该计划支出能否满足一年的养护需要?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国“蛟龙”号深潜器目前最大深潜极限为7062.68米.如图,某天该深潜器在海面下2000米的A点处作业,测得俯角为30°正前方的海底C点处有黑匣子信号发出.该深潜器受外力作用可继续在同一深度直线航行3000米后,再次在B点处测得俯角为45°正前方的海底C点处有黑匣子信号发出,请通过计算判断“蛟龙”号能否在保证安全的情况下打捞海底黑匣子.(参考数据![]() ≈1.732)
≈1.732)
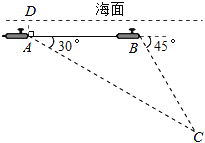
查看答案和解析>>
科目:初中数学 来源: 题型:
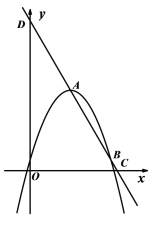
【题目】如图所示,二次函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于A、B两点,点B在点A的右侧,直线AB分别交x轴、y轴于C、D两点,且k<0.
的图象交于A、B两点,点B在点A的右侧,直线AB分别交x轴、y轴于C、D两点,且k<0.
(1)求A,B两点横坐标;
(2)若△OAB是以OA为腰的等腰三角形,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了创建文明城市,增弘环保意识,某班随机抽取了8名学生(分别为A,B,C,D,E,F,G,H),进行垃圾分类投放检测,检测结果如下表,其中“√”表示投放正确,“×”表示投放错误,
学生 垃圾类别 | A | B | C | D | E | F | G | H |
可回收物 | √ | × | × | √ | √ | × | √ | √ |
其他垃圾 | × | √ | √ | √ | √ | × | √ | √ |
餐厨垃圾 | √ | √ | √ | √ | √ | √ | √ | √ |
有害垃圾 | × | √ | × | × | × | √ | × | √ |
(1)检测结果中,有几名学生正确投放了至少三类垃圾?请列举出这几名学生.
(2)为进一步了解学生垃圾分类的投放情况,从检测结果是“有害垃圾”投放错误的学生中随机抽取2名进行访谈,求抽到学生A的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠MON=120°,点A,B分别在ON,OM边上,且OA=OB,点C在线段OB上(不与点O,B重合),连接CA.将射线CA绕点C逆时针旋转120°得到射线CA′,将射线BO绕点B逆时针旋转150°与射线CA′交于点D.

(1)根据题意补全图1;
(2)求证:
①∠OAC=∠DCB;
②CD=CA(提示:可以在OA上截取OE=OC,连接CE);
(3)点H在线段AO的延长线上,当线段OH,OC,OA满足什么等量关系时,对于任意的点C都有∠DCH=2∠DAH,写出你的猜想并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com