
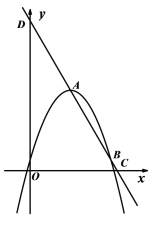
【题目】如图所示,二次函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于A、B两点,点B在点A的右侧,直线AB分别交x轴、y轴于C、D两点,且k<0.
的图象交于A、B两点,点B在点A的右侧,直线AB分别交x轴、y轴于C、D两点,且k<0.
(1)求A,B两点横坐标;
(2)若△OAB是以OA为腰的等腰三角形,求k的值.
 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
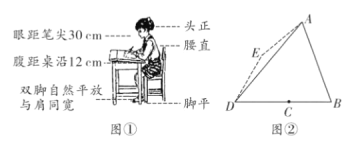
【题目】良好的坐姿习惯有利于青少年骨骼生长,有利于身体健康,那么首先要有正确的写字坐姿,身体上半部坐直,头部端正、目视前方,两手放在桌面上,两腿平放,胸膛挺起,理想状态下,如图①,将图①中的眼睛记为点![]() ,腹部记为点
,腹部记为点![]() ,笔尖记为点
,笔尖记为点![]() ,且
,且![]() 与桌面沿的交点记为点
与桌面沿的交点记为点![]() ,已知
,已知![]() ,点
,点![]() 到
到![]() 的距离为23cm,
的距离为23cm, ![]() .
.
(1)求![]() 的度数
的度数
(2)老师发现小亮同学写字姿势不正确,眼睛倾斜到图2的点![]() ,点
,点![]() 恰好在
恰好在![]() 的垂直平分线上,且
的垂直平分线上,且![]() ,于是要求其纠正为正确的姿势,求眼睛所在的位置上升的距离(结果精确到1cm)
,于是要求其纠正为正确的姿势,求眼睛所在的位置上升的距离(结果精确到1cm)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△AOB与△A1OB1是以点O为位似中心的位似图形,且相似比为1:2,点B的坐标为(-1,2),则点B1的坐标为( )

A.(2,-4)B.(1,-4)C.(-1,4)D.(-4,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
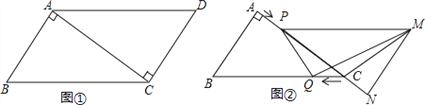
【题目】已知,如图①,在ABCD中,AB=3cm,BC=5cm,AC⊥AB,△ACD沿AC的方向匀速平移得到△PNM,速度为1cm/s;同时,点Q从点C出发,沿CB方向匀速移动,速度为1cm/s,当△PNM停止平移时,点Q也停止移动,如图②,设移动时间为t(s)(0<t<4),连接PQ,MQ,MC,解答下列问题:
(1)当t为何值时,PQ∥MN?
(2)设△QMC的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使S△QMC:S四边形ABQP=1:4?若存在,求出t的值;若不存在,请说明理由.
(4)是否存在某一时刻t,使PQ⊥MQ?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
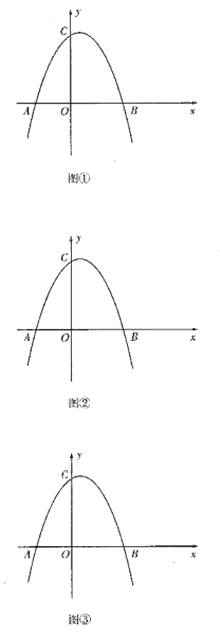
【题目】如图,抛物线交![]() 轴于
轴于![]() ,
,![]() ,交
,交![]() 轴于
轴于![]() .
.
(1)求抛物线解析式;
(2)点![]() 在第一象限的抛物线上,
在第一象限的抛物线上,![]() 与
与![]() 的面积比为
的面积比为![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在(2)的条件下,在点![]() 与
与![]() 之间的抛物线上取点
之间的抛物线上取点![]() ,
,![]() 交
交![]() 于
于![]() ,
,![]() 交
交![]() 轴于
轴于![]() 、交
、交![]() 延长线于
延长线于![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
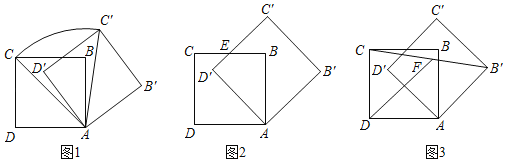
【题目】若边长为6的正方形ABCD绕点A顺时针旋转,得正方形AB′C′D′,记旋转角为a.
(I)如图1,当a=60°时,求点C经过的弧![]() 的长度和线段AC扫过的扇形面积;
的长度和线段AC扫过的扇形面积;
(Ⅱ)如图2,当a=45°时,BC与D′C′的交点为E,求线段D′E的长度;
(Ⅲ)如图3,在旋转过程中,若F为线段CB′的中点,求线段DF长度的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】1637年笛卡儿(R.Descartes,1596-1650)在其《几何学》中,首次应用待定系数法最早给出因式分解定理.关于笛卡尔的“待定系数法”原理,举例说明如下:
分解因式:![]() .观察知,显然
.观察知,显然![]() 时,原式
时,原式![]() ,因此原式可分解为
,因此原式可分解为![]() 与另一个整式的积.令:
与另一个整式的积.令:![]() ,而
,而![]() ,因等式两边
,因等式两边![]() 同次幂的系数相等,则有:
同次幂的系数相等,则有: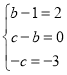 ,得
,得![]() ,从而
,从而![]()
根据以上材料,理解并运用材料提供的方法,解答以下问题:
(1)若![]() 是多项式
是多项式![]() 的因式,求
的因式,求![]() 的值并将多项式
的值并将多项式![]() 分解因式.
分解因式.
(2)若多项式![]() 含有因式
含有因式![]() 及
及![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
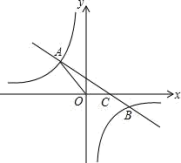
【题目】如图,一次函数y=kx+b(k≠0)的图象与反比例函数![]() 的图象交于二、四象限内的A、B两点,与x轴交于C点,点A的坐标为(﹣2,3),点B的坐标为(4,n).
的图象交于二、四象限内的A、B两点,与x轴交于C点,点A的坐标为(﹣2,3),点B的坐标为(4,n).
(1)求该反比例函数和一次函数的解析式;
(2)在x轴上是否存在点P,使△APC是直角三角形?若存,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com