
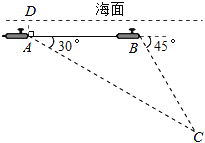
【题目】中国“蛟龙”号深潜器目前最大深潜极限为7062.68米.如图,某天该深潜器在海面下2000米的A点处作业,测得俯角为30°正前方的海底C点处有黑匣子信号发出.该深潜器受外力作用可继续在同一深度直线航行3000米后,再次在B点处测得俯角为45°正前方的海底C点处有黑匣子信号发出,请通过计算判断“蛟龙”号能否在保证安全的情况下打捞海底黑匣子.(参考数据![]() ≈1.732)
≈1.732)
【答案】“蛟龙”号能在保证安全的情况下打捞海底黑匣子.
【解析】
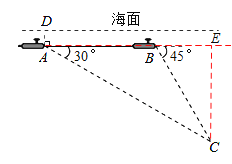
试题过点C作CE⊥AB交AB延长线于E,设CE=x,在Rt△BCE和Rt△ACE中分别用x表示BE和AE的长度,然后根据AB+BE=AE,列出方程求出x的值,继而可判断“蛟龙”号能在保证安全的情况下打捞海底黑匣子C.
试题解析:解:如答图,过点C作CE⊥AB交AB延长线于E,
设CE=x,
在Rt△BCE中,∵∠CBE=45°,∴BE=CE=x.
在Rt△ACE中,∵∠CAE=30°,∴AE=![]() x.
x.
∵AB+BE=AE,
∴3000+x=![]() x,
x,
解得:x=1500(![]() +1)≈4098(米),
+1)≈4098(米),
∵2000+4098=6098<7062.68,
∴“蛟龙”号能在保证安全的情况下打捞海底黑匣子.


科目:初中数学 来源: 题型:
【题目】四边形 ABCD 中,E 为边 BC 上一点,F 为边 CD 上一点,且∠AEF=90°.
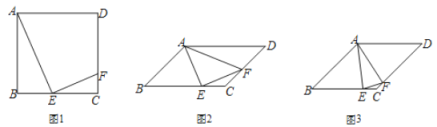
(1)如图 1,若 ABCD 为正方形,E 为 BC 中点,求证:![]() .
.
(2)若 ABCD 为平行四边形,∠AFE=∠ADC,
①如图 2,若∠AFE=60°,求![]() 的值;
的值;
②如图 3,若 AB=BC,EC=2CF.直接写出 cos∠AFE 值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
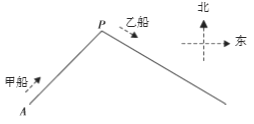
【题目】小岛![]() 在港口
在港口![]() 的南偏西45°方向,距离港口81海里处.甲船从
的南偏西45°方向,距离港口81海里处.甲船从![]() 出发,沿
出发,沿![]() 方向以6海里/时的速度驶向港口,乙船从港口
方向以6海里/时的速度驶向港口,乙船从港口![]() 出发,沿南偏东60°方向,以15海里/时的速度驶离港口.现两船同时出发.
出发,沿南偏东60°方向,以15海里/时的速度驶离港口.现两船同时出发.
(1)出发后 小时两船与港口![]() 的距离相等;
的距离相等;
(2)出发几小时后乙船在甲船的正东方向?(结果精确到0.1小时,参考数据:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
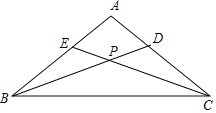
【题目】如图,在等腰△ABC中,AB=AC,CE、BD分别为∠ACB、∠ABC的角平分线,CE、BD相交于P.
(1)求证:CD=BE;
(2)若∠A=98°,求∠BPC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△AOB与△A1OB1是以点O为位似中心的位似图形,且相似比为1:2,点B的坐标为(-1,2),则点B1的坐标为( )

A.(2,-4)B.(1,-4)C.(-1,4)D.(-4,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
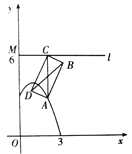
【题目】如图,点A在抛物线![]() 上,直线
上,直线![]() ⊥y轴于点M,AC⊥
⊥y轴于点M,AC⊥![]() 于点C,以AC为对角线作矩形ABCD,若点M的坐标为(0,6),则BD的取值范围是_______.
于点C,以AC为对角线作矩形ABCD,若点M的坐标为(0,6),则BD的取值范围是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
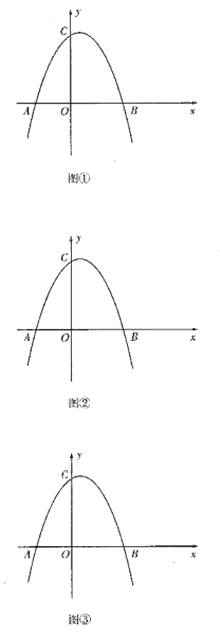
【题目】如图,抛物线交![]() 轴于
轴于![]() ,
,![]() ,交
,交![]() 轴于
轴于![]() .
.
(1)求抛物线解析式;
(2)点![]() 在第一象限的抛物线上,
在第一象限的抛物线上,![]() 与
与![]() 的面积比为
的面积比为![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在(2)的条件下,在点![]() 与
与![]() 之间的抛物线上取点
之间的抛物线上取点![]() ,
,![]() 交
交![]() 于
于![]() ,
,![]() 交
交![]() 轴于
轴于![]() 、交
、交![]() 延长线于
延长线于![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
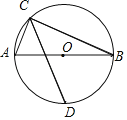
【题目】如图,AB是⊙O的直径,点C是⊙O上一点(点C不与A,B重合),连接CA,CB.∠ACB的平分线CD与⊙O交于点D.
(1)求∠ACD的度数;
(2)探究CA,CB,CD三者之间的等量关系,并证明;
(3)E为⊙O外一点,满足ED=BD,AB=5,AE=3,若点P为AE中点,求PO的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
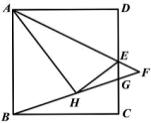
【题目】如图,在正方形ABCD中,AB=2,点E是CD的中点,连接AE,将△ADE沿AE折叠至△AHE,连接BH,延长AE,BH交于点F;BF,CD交于点G,则FG=_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com