
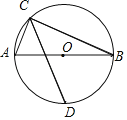
【题目】如图,AB是⊙O的直径,点C是⊙O上一点(点C不与A,B重合),连接CA,CB.∠ACB的平分线CD与⊙O交于点D.
(1)求∠ACD的度数;
(2)探究CA,CB,CD三者之间的等量关系,并证明;
(3)E为⊙O外一点,满足ED=BD,AB=5,AE=3,若点P为AE中点,求PO的长.
【答案】(1)∠ACD=45°;(2)BC+AC=![]() CD,见解析;(3)OP=
CD,见解析;(3)OP=![]() .
.
【解析】
(1)由圆周角的定义可求∠ACB=90°,再由角平分线的定义得到∠ACD=45°;
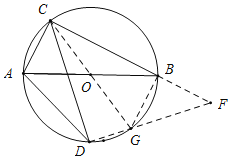
(2)连接CO延长与圆O交于点G,连接DG、BG,延长DG、CB交于点F;先证明△BGF是等腰直角三角形,得到BG=BF,AG=BF,再证明△CDF是等腰三角三角形,得到CF=![]() CD,即可求得BC+AC=
CD,即可求得BC+AC=![]() CD;
CD;
(3)过点A作AM⊥ED,过点B作BN⊥ED交ED延长线与点N,连接BE;先证明Rt△AMD≌Rt△DNB(AAS),再证明△AED是等腰三角形,分别求得EN=![]() ,BN=
,BN=![]() ,在Rt△EBN中,BE=
,在Rt△EBN中,BE=![]() ,OP=
,OP=![]() BN=
BN=![]() .
.
解:(1)∵AB是直径,点C在圆上,
∴∠ACB=90°,
∵∠ACB的平分线CD与⊙O交于点D,
∴∠ACD=45°;
(2)BC+AC=![]() CD,
CD,
连接CO延长与圆O交于点G,连接DG、BG,延长DG、CB交于点F;
∴∠CDG=∠CBG=90°,
∵∠ACB=90°,
∴AC∥BG,
∴∠CGB=∠ACG,
∴∠CGB=45°+∠DCG,
∵∠CBF=90°+∠DCG,
∴∠BGF=45°,
∴△BGF是等腰直角三角形,
∴BG=BF,
∵△ACO≌△BGO(SAS),
∴AG=BF,
∵△CDF是等腰三角三角形,
∴CF=![]() CD,
CD,
∴BC+AC=![]() CD;
CD;
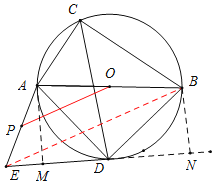
(3)过点A作AM⊥ED,过点B作BN⊥ED交ED延长线与点N,连接BE;
∵∠ACD=∠ABD=45°,∠ADB=90°,
∴AD=BD,
∵AB=5,
∴BD=AD=
∵∠MAD=∠BDN,
∴Rt△AMD≌Rt△DNB(AAS),
∴AM=DN,MD=BN,
∵ED=BD,
∴△AED是等腰三角形,
∵AE=3,
∴AM=![]() ,DM=
,DM=![]() ,
,
∴EN=![]() ,BN=
,BN=![]() ,
,
在Rt△EBN中,BE=![]() ,
,
∵P是AE的中点,O是AB的中点,
∴OP=![]() BN,
BN,
∴OP=![]() .
.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=x+2与x轴交于点A,与y轴交于点C,与反比例函数y=![]() 在第一象限内的图象交于点B(1,3),连接BO,下面三个结论:①S△AOB=1.5;②点(x1,y1)和点(x2,y2)在反比例函数的图象上,若x1>x2,则y1<y2;③不等式x+2<
在第一象限内的图象交于点B(1,3),连接BO,下面三个结论:①S△AOB=1.5;②点(x1,y1)和点(x2,y2)在反比例函数的图象上,若x1>x2,则y1<y2;③不等式x+2<![]() 的解集是0<x<1.其中正确的有( )
的解集是0<x<1.其中正确的有( )
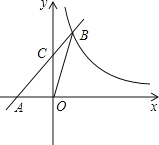
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
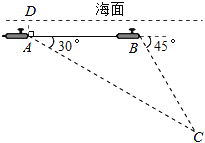
【题目】中国“蛟龙”号深潜器目前最大深潜极限为7062.68米.如图,某天该深潜器在海面下2000米的A点处作业,测得俯角为30°正前方的海底C点处有黑匣子信号发出.该深潜器受外力作用可继续在同一深度直线航行3000米后,再次在B点处测得俯角为45°正前方的海底C点处有黑匣子信号发出,请通过计算判断“蛟龙”号能否在保证安全的情况下打捞海底黑匣子.(参考数据![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
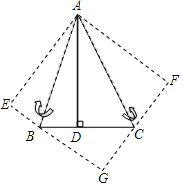
【题目】如图,△ABC中,已知∠BAC=45°,AD⊥BC于D,BD=2,DC=3,把△ABD、△ACD分别以AB、AC为对称轴翻折变换,D点的对称点为E、F,延长EB、FC相交于G点.
(1)求证:四边形AEGF是正方形;
(2)求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了创建文明城市,增弘环保意识,某班随机抽取了8名学生(分别为A,B,C,D,E,F,G,H),进行垃圾分类投放检测,检测结果如下表,其中“√”表示投放正确,“×”表示投放错误,
学生 垃圾类别 | A | B | C | D | E | F | G | H |
可回收物 | √ | × | × | √ | √ | × | √ | √ |
其他垃圾 | × | √ | √ | √ | √ | × | √ | √ |
餐厨垃圾 | √ | √ | √ | √ | √ | √ | √ | √ |
有害垃圾 | × | √ | × | × | × | √ | × | √ |
(1)检测结果中,有几名学生正确投放了至少三类垃圾?请列举出这几名学生.
(2)为进一步了解学生垃圾分类的投放情况,从检测结果是“有害垃圾”投放错误的学生中随机抽取2名进行访谈,求抽到学生A的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在数轴上点![]() 表示数
表示数![]() ,点
,点![]() 表示数
表示数![]() ,点
,点![]() 表示数
表示数![]() 是最大的负整数,且
是最大的负整数,且![]() 满足
满足![]() .
.
![]()
(1)a=________,b=________,c=________.
(2)若将数轴折叠,使得点![]() 与点
与点![]() 重合,则点
重合,则点![]() 与数________表示的点重合;
与数________表示的点重合;
(3)点![]() 开始在数轴上运动,若点
开始在数轴上运动,若点![]() 以每秒1个单位长度的速度向左运动,同时,点
以每秒1个单位长度的速度向左运动,同时,点![]() 和点
和点![]() 分别以每秒2个单位长度和3个单位长度的速度向右运动,假设
分别以每秒2个单位长度和3个单位长度的速度向右运动,假设![]() 秒钟过后,若点
秒钟过后,若点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,则
,则![]() ________,
________,![]() ________.(用含
________.(用含![]() 的代数式表示)
的代数式表示)
(4)![]() 的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值。
的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了丰富学生课余生活,开展了“第二课堂”活动,推出了以下四种选修课程:![]() .绘画;
.绘画;![]() .唱歌;
.唱歌;![]() .跳舞;
.跳舞;![]() .演讲;
.演讲;![]() .书法.学校规定:每个学生都必须报名且只能选择其中的一个课程.学校随机抽查了部分学生,对他们选择的课程情况进行了统计,并绘制了如下两幅不完整的统计图.
.书法.学校规定:每个学生都必须报名且只能选择其中的一个课程.学校随机抽查了部分学生,对他们选择的课程情况进行了统计,并绘制了如下两幅不完整的统计图.
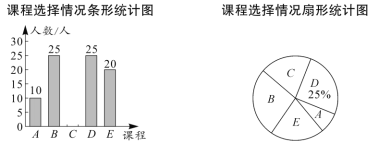
请结合统计图中的信息解决下列问题:
(1)这次抽查的学生人数是多少人?
(2)将条形统计图补充完整.
(3)求扇形统计图中课程![]() 所对应扇形的圆心角的度数.
所对应扇形的圆心角的度数.
(4)如果该校共有1200名学生,请你估计该校选择课程![]() 的学生约有多少人.
的学生约有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小东设计的“过直线外一点作这条直线的平行线”的尺规作图过程.
已知:直线及直线外一点![]() .
.

求作:![]() ,使得
,使得![]() .
.
作法:如图,
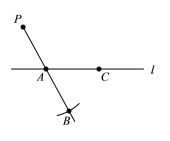
①在直线上取一点![]() ,作射线
,作射线![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 长为半径画弧,交
长为半径画弧,交![]() 的延长线于点
的延长线于点![]() ;
;
②在直线上取一点![]() (不与点
(不与点![]() 重合),作射线
重合),作射线![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 长为半径画弧,交
长为半径画弧,交![]() 的延长线于点
的延长线于点![]() ;
;
③作直线![]() .
.
所以直线![]() 就是所求作的直线.
就是所求作的直线.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵![]() _______,
_______,![]() _______,
_______,
∴![]() (____________)(填推理的依据).
(____________)(填推理的依据).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图形都是由面积为1的正方形按一定的规律组成,其中,第(1)个图形中面积为1的正方形有2个,第(2)个图形中面积为1的正方形有5个,第(3)个图形中面积为1的正方形有9个,按此规律,则第(6)个图形中面积为1的正方形的个数为( )

A.14B.20C.24D.27
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com